Résoudre des problèmes fonctionnellement

Dans ce chapitre, nous allons regarder quelques problèmes intéressants et comment les résoudre fonctionnellement et aussi élégamment que possible. On ne découvrira probablement pas de nouveau concept, on va juste échauffer nos muscles Haskell tout fraîchement acquis et s’entraîner à coder. Chaque section présentera un problème différent. On commencera par décrire le problème, puis on essaiera de trouver le meilleur moyen de le résoudre (ou le moins mauvais).

Calculatrice de notation polonaise inverse

Généralement, lorsqu’on écrit des expressions mathématiques à l’école, on les écrit de manière infixe. Par exemple, on écrit 10 - (4 + 3) * 2. +, * et - sont des opérateurs infixes, tout comme les fonctions infixes qu’on a rencontrées en Haskell (+, `elem`, etc.). C’est pratique puisqu’en tant qu’humains, il nous est facile de décomposer cette expression dans notre esprit. L’inconvénient, c’est qu’on a besoin de parenthèses pour indiquer la précédence.

La notation polonaise inverse est une autre façon d’écrire les expressions mathématiques. Au départ, ça semble un peu bizarre, mais c’est en fait assez simple à comprendre et à utiliser puisqu’il n’y a pas besoin de parenthèses, et parce que c’est très simple à taper dans une calculatrice. Bien que la plupart des calculatrices modernes utilisent la notation infixe, certaines personnes ne jurent toujours que par leur calculatrice NPI. Voici ce à quoi l’expression infixe précédente ressemble en NPI : 10 4 3 + 2 * -. Comment calcule-t-on le résultat de cela ? Eh bien, imaginez une pile. Vous parcourez l’expression de gauche à droite. Chaque fois qu’un nombre est rencontré, vous l’empilez. Dès que vous rencontrez un opérateur, vous retirez les deux nombres en sommet de pile (on dit aussi qu’on les dépile), utilisez l’opérateur sur ces deux nombres, et empilez le résultat. Si l’expression est bien formée, en arrivant à la fin vous ne devriez plus avoir qu’un nombre dans la pile, et ce nombre est le résultat.

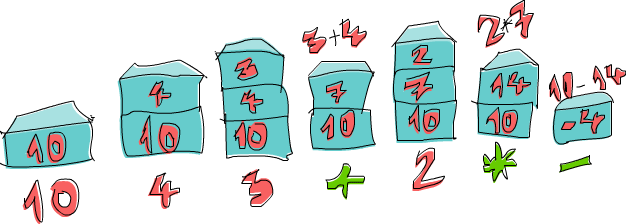
Parcourons l’expression 10 4 3 + 2 * - ensemble ! D’abord, on empile 10, et la pile est donc 10. Le prochain élément est 4, on l’empile également. La pile est maintenant 10, 4. De même avec 3, la pile est à présent 10, 4, 3. Soudain, on rencontre un opérateur, j’ai nommé + ! On dépile les deux nombres au sommet de la pile (donc la pile devient 10), on somme ces deux nombres, et on empile le résultat. La pile est désormais 10, 7. On empile le 2, la pile devient 10, 7, 2. On rencontre un nouvel opérateur, on dépile donc 7 et 2, on les multiplie et on empile le résultat. 7 fois 2 donne 14, la pile est donc 10, 14. Finalement, il y a un -. On dépile 10 et 14, on soustrait 14 de 10 et on empile le résultat. La pile est maintenant -4, et puisqu’il n’y a plus de nombres ou d’opérateurs dans notre expression, c’est notre résultat !

Maintenant qu’on sait calculer n’importe quelle expression NPI à la main, réfléchissons à une manière d’écrire une fonction Haskell qui prendrait en paramètre une chaîne de caractères contenant une expression NPI, comme "10 4 3 + 2 * -", et nous renvoie son résultat.

Quel serait le type d’une telle fonction ? On veut qu’elle prenne une chaîne de caractères en paramètre, et produise un nombre en résultat. Ce sera donc probablement quelque chose comme solveRPN :: (Num a) => String -> a (NDT : “RPN” pour “Reverse Polish Notation”).

Cool. Quand on implémente une solution à un problème en Haskell, il est aussi bien de penser à la façon dont vous le feriez à la main et d’en tirer des idées. Ici, on voit qu’on traite chaque nombre ou opérateur séparé par une espace comme un élément unique. Il serait donc peut-être utile de commencer par découper une chaîne comme "10 4 3 + 2 * -" en une liste d’éléments comme ["10","4","3","+","2","*","-"].

Ensuite, que faisions-nous avec cette liste d’éléments dans notre tête ? On la parcourait de la gauche vers la droite, et on maintenait une pile tout du long. Est-ce que cette phrase vous rappelle quelque chose ? Souvenez-vous, dans la section sur les plis, on a dit que quasiment toute fonction qui traverse une liste de gauche à droite ou de droite à gauche, élément par élément, et construit (accumule) un résultat (que ce soit un nombre, une liste, une pile, peu importe), peut être implémentée comme un pli.

Dans ce cas, on va utiliser un pli gauche, puisqu’on traverse la liste de la gauche vers la droite. La valeur de l’accumulateur sera notre pile et ainsi, le résultat du pli sera aussi une pile, seulement, comme on l’a vu, elle ne contiendra qu’un élément.

Une autre chose à pondérer est, eh bien, comment va-t-on représenter cette pile ? Je propose d’utiliser une liste. Également, je propose de garder la somme de notre pile du côté de la tête de la liste. C’est parce qu’ajouter en tête (début) de liste est bien plus rapide que d’ajouter à la fin. Donc si l’on a une pile qui consiste en, mettons, 10, 4, 3, nous la représenterons comme la liste [3, 4, 10].

On a à présent assez d’informations pour ébaucher notre fonction. Elle va prendre une liste, comme "10 4 3 + 2 * -" et la décomposer en liste d’éléments en utilisant words pour obtenir ["10","4","3","+","2","*","-"]. Ensuite, on va utiliser un pli gauche sur la liste et terminer avec une pile à un seul élément, [-4]. On sort cet élément de la liste, et c’est notre résultat final !

Voici donc l’esquisse de notre fonction :

import Data.List

solveRPN :: (Num a) => String -> a
solveRPN expression = head (foldl foldingFunction [] (words expression))
    where   foldingFunction stack item = ...

On prend l’expression et on la change en une liste d’éléments. Puis on plie la liste d’éléments avec la fonction de pli. Remarquez le [], qui représente l’accumulateur initial. L’accumulateur est notre pile, donc [] représente une pile vide, avec laquelle on débute. Une fois qu’on récupère la pile finale qui ne contient qu’un élément, on appelle head sur cette liste pour obtenir cet élément, et on applique read.

Tout ce qu’il reste à faire consiste à implémenter une fonction de pli qui va prendre une pile, comme [4, 10], et un élément, comme "3", et retourner une nouvelle pile [3, 4, 10]. Si la pile est [4, 10] et que l’élément est "*", alors elle devra retourner [40]. Mais avant cela, transformons notre fonction en style sans point, parce qu’elle est pleine de parenthèses qui m’effraient :

import Data.List

solveRPN :: (Num a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction stack item = ...

Ah, nous voilà. Beaucoup mieux. Ainsi, la fonction de pli prend une pile et un élément et retourne une nouvelle pile. On va utiliser du filtrage par motif pour obtenir les deux éléments en haut de pile, et filtrer les opérateurs comme "*" et "-".

solveRPN :: (Num a, Read a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction (x:y:ys) "*" = (x * y):ys
            foldingFunction (x:y:ys) "+" = (x + y):ys
            foldingFunction (x:y:ys) "-" = (y - x):ys
            foldingFunction xs numberString = read numberString:xs

On a étendu cela sur quatre motifs. Les motifs seront essayés de haut en bas. D’abord, la fonction de pli regarde si l’élément courant est "*". Si c’est le cas, alors elle prendra une liste comme [3, 4, 9, 3] et nommera ses deux premiers éléments x et y respectivement. Dans ce cas, x serait 3 et y serait 4. ys serait [9, 3]. Elle retourne une liste comme ys, mais avec le produit de x et y en tête. Ainsi, on a dépilé les deux nombres en haut de pile, on les a multipliés et on a empilé le résultat. Si l’élément n’est pas "*", le filtrage par motif continue avec le motif "+", et ainsi de suite.

Si l’élément n’est aucun des opérateurs, alors on suppose que c’est une chaîne qui représente un nombre. Si c’est un nombre, on appelle read sur la chaîne pour obtenir un nombre, et on retourne la pile précédente avec ce nombre empilé.

Et c’est tout ! Remarquez aussi qu’on a ajouté une contrainte de classe supplémentaire Read a à la déclaration de type de la fonction, parce qu’on appelle read sur la chaîne de caractères pour obtenir le nombre. Ainsi, cette déclaration signifie que le résultat peut être de n’importe quel type membre des classes de types Num et Read (comme Int, Float, etc.).

Pour la liste d’éléments ["2", "3", "+"], notre fonction va commencer à plier par la gauche. La pile initiale sera []. Elle appellera la fonction de pli avec [] en tant que pile (accumulateur) et "2" en tant qu’élément. Puisque cet élément n’est pas un opérateur, il sera lu avec read et ajouté au début de []. La nouvelle pile est donc [2], et la fonction de pli sera appelée avec [2] pour pile et ["3"] pour élément, produisant une nouvelle pile [3, 2]. Ensuite, elle est appelée pour la troisième fois avec [3, 2] pour pile et "+" pour élément. Cela cause le dépilement des deux nombres, qui sont alors sommés, et leur résultat est empilé. La pile finale est [5], qui est le nombre qu’on retourne.

Jouons avec notre fonction :

ghci> solveRPN "10 4 3 + 2 * -"
-4
ghci> solveRPN "2 3 +"
5
ghci> solveRPN "90 34 12 33 55 66 + * - +"
-3947
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 3 -"
87

Cool, elle marche ! Une chose sympa avec cette fonction, c’est qu’elle peut être facilement modifiée pour supporter une variété d’autres opérateurs. Ils n’ont même pas besoin d’être binaires. Par exemple, on peut créer un opérateur "log" qui ne dépile qu’un nombre, et empile son logarithme. On peut aussi faire un opérateur ternaire qui dépile trois nombres et empile le résultat, comme "sum" qui dépile tous les nombres et empile leur somme.

Modifions notre fonction pour gérer quelques nouveaux opérateurs. Par simplicité, on va changer sa déclaration de type pour qu’elle retourne un type Float.

import Data.List

solveRPN :: String -> Float
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction (x:y:ys) "*" = (x * y):ys
            foldingFunction (x:y:ys) "+" = (x + y):ys
            foldingFunction (x:y:ys) "-" = (y - x):ys
            foldingFunction (x:y:ys) "/" = (y / x):ys
            foldingFunction (x:y:ys) "^" = (y ** x):ys
            foldingFunction (x:xs) "ln" = log x:xs
            foldingFunction xs "sum" = [sum xs]
            foldingFunction xs numberString = read numberString:xs

Wow, génial ! / est la division bien sûr, et ** est l’exponentiation des nombres à virgule flottante. Pour l’opérateur logarithme, on filtre avec un motif à un seul élément parce qu’on n’a besoin que d’un élément pour calculer un logarithme naturel. Avec l’opérateur de somme, on retourne une pile qui n’a qu’un élément, égal à la somme de tout ce que contenait la pile jusqu’alors.

ghci> solveRPN "2.7 ln"
0.9932518
ghci> solveRPN "10 10 10 10 sum 4 /"
10.0
ghci> solveRPN "10 10 10 10 10 sum 4 /"
12.5
ghci> solveRPN "10 2 ^"
100.0

Remarquez qu’on peut inclure des nombres à virgule flottante dans nos expressions parce que read sait comment les lire.

ghci> solveRPN "43.2425 0.5 ^"
6.575903

Je pense que faire une fonction qui calcule des expressions arbitraires sur les nombres à virgule flottante en NPI, et qui peut être facilement extensible, en une dizaine de lignes, est plutôt génial.

Une chose à noter à propos de cette fonction est qu’elle n’est pas très résistante aux erreurs. Si on lui donne une entrée qui n’a pas de sens, cela va juste tout planter. On fera une version résistante aux erreurs de cette fonction qui aura pour déclaration de type solveRPN :: String -> Maybe Float une fois qu’on aura découvert les monades (elles ne sont pas effrayantes, faites-moi confiance !). On pourrait en écrire une dès maintenant, mais ce serait un peu fastidieux parce qu’il faudrait vérifier les valeurs Nothing à chaque étape. Toutefois, si vous vous sentez d’humeur pour le défi, vous pouvez vous lancer ! Indice : vous pouvez utiliser reads pour voir si un read a réussi ou non.

D’Heathrow à Londres

Notre prochain problème est le suivant : votre avion vient d’atterrir en Angleterre, et vous louez une voiture. Vous avez un rendez-vous très bientôt, et devez aller de l’aéroport d’Heathrow jusqu’à Londres aussi vite que possible (mais sans vous mettre en danger !).

Il y a deux routes principales allant d’Heathrow à Londres, et un nombre de routes régionales qui croisent celles-ci. Il vous faut une quantité de temps fixe pour voyager d’une intersection à une autre. Vous devez trouver le chemin optimal pour arriver à Londres aussi vite que possible ! Vous partez du côté gauche et pouvez soit changer de route principale, soit rouler vers Londres.

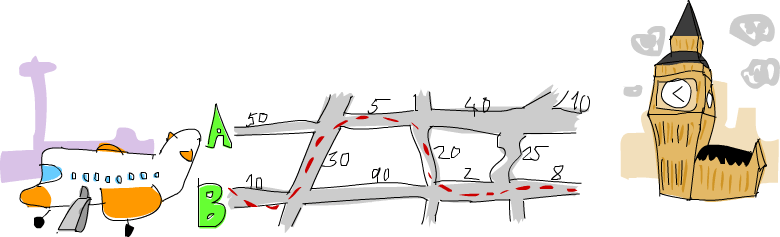
Comme vous le voyez sur l’image, le chemin le plus court d’Heathrow à Londres dans ce cas consiste à démarrer sur la route principale B, changer de route principale, avancer sur A, changer à nouveau, et continuer jusqu’à Londres sur la route B. En prenant ce chemin, il nous faut 75 minutes. Si on en avait choisi un autre, il nous faudrait plus longtemps que ça.

Notre travail consiste à créer un programme qui prend une entrée représentant un système routier, et affiche le chemin le plus court pour le traverser. Voici à quoi ressemblera l’entrée dans ce cas :

50
10
30
5
90
20
40
2
25
10
8
0

Pour découper mentalement le fichier d’entrée, lisez-le trois lignes par trois lignes, et coupez mentalement le système routier en sections. Chaque section se compose d’un morceau de route A, d’un morceau de route B, et d’une route croisant A et B. Pour conserver cette lecture trois par trois, on dit qu’il y a une dernière route transversale qui prend 0 minute à traverser. Parce qu’une fois arrivé à Londres, ce n’est plus important, on est arrivé.

Tout comme on l’a fait en résolvant le problème de la calculatrice NPI, on va résoudre ce problème en trois étapes :

• Oublier Haskell un instant et penser à la résolution du problème à la main
• Penser à la représentation des données en Haskell
• Trouver comment opérer sur les données en Haskell pour aboutir à la solution

Dans la section sur la calculatrice NPI, on a d’abord remarqué qu’en calculant une expression à la main, on avait gardé une sorte de pile dans notre esprit et traversé l’expression un élément à la fois. On a décidé d’utiliser une liste de chaînes de caractères pour représenter l’expression. Finalement, on a utilisé un pli gauche pour traverser la liste de chaînes tout en maintenant la pile pour produire la solution.

Ok, donc, comment trouverions-nous le plus court chemin d’Heathrow à Londres à la main ? Eh bien, on peut prendre du recul, essayer de deviner ce plus court chemin, et avec un peu de chance on trouvera le bon résultat. Cette solution fonctionne pour de petites entrées, mais qu’en sera-t-il si notre route a 10 000 sections ? Ouf ! On ne saura pas non plus dire avec certitude que notre solution est optimale, on pourra simplement se dire qu’on en est plutôt sûr.

Ce n’est donc pas une bonne solution. Voici une image simplifiée de notre système routier :

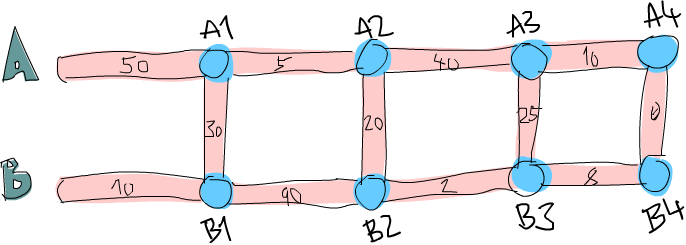
Parfait, pouvez-vous trouver quel est le plus court chemin jusqu’à la première intersection de la route A (le premier point bleu sur la route A, noté A1) ? C’est plutôt trivial. On regarde simplement s’il est plus court d’y aller directement depuis A, ou de passer par B puis traverser. Évidemment, il vaut mieux passer par B et traverser, puisque cela prend 40 minutes, alors qu’il faut 50 minutes depuis A. Qu’en est-il du plus court chemin vers B1 ? La même chose. On voit qu’il est beaucoup plus court de passer par B (10 minutes) que de passer par A et traverser, ce qui nous prendrait 80 minutes !

À présent, on connaît le chemin le plus court jusqu’à A1 (passer par B et traverser, on va dire B, C avec un coût de 40 minutes) et on connaît le plus court chemin jusqu’à B1 (directement par B, donc B, en 10 minutes). Est-ce que ce savoir nous aide pour connaître le chemin le plus court jusqu’à la prochaine intersection de chacune des routes principales ? Mon dieu, mais c’est bien sûr !

Voyons ce que serait le plus court chemin jusqu’à A2. Pour aller à A2, on peut soit aller directement d’A1 à A2, soit avancer depuis B1 et traverser (souvenez-vous, on ne peut qu’avancer ou traverser). Et puisqu’on connaît les coûts d’A1 et B1, on peut facilement trouver le meilleur chemin jusqu’à A2. Il faut 40 minutes pour aller à A1, puis 5 minutes d’A1 à A2, donc B, C, A coûte 45 minutes. Il ne coûte que 10 minutes pour aller à B2, mais il faut 110 minutes supplémentaires pour avancer jusqu’à B2 puis traverser ! Évidemment, le chemin le plus court jusqu’à A2 est B, C, A. De la même façon, le chemin le plus court jusqu’à B2 consiste à aller tout droit depuis A1 et traverser.

À présent qu’on connaît les meilleurs chemins pour aller à A2 et à B2, on peut répéter le processus indéfiniment jusqu’à atteindre l’arrivée. Une fois qu’on connaît les meilleurs chemins pour A4 et B4, le moins coûteux sera notre chemin optimal.

En gros, pour la deuxième section, on répète ce qu’on a fait pour la première section, mais en prenant en compte les meilleurs chemins précédents pour A comme pour B. On pourrait dire qu’on a aussi pris en compte les meilleurs chemins précédents à la première étape, en considérant que ces chemins vides avaient un coût de 0.

Voilà un résumé. Pour trouver le meilleur chemin d’Heathrow à Londres, on procède ainsi : d’abord, on cherche le meilleur chemin jusqu’à la prochaine intersection de la route A. Il n’y a que deux options : aller directement tout droit, ou commencer de la route opposée, avancer puis traverser. On se souvient du meiller chemin et du coût. On utilise la même méthode pour trouver le meilleur chemin jusqu’à la prochaine intersection de la route B. Ensuite, on se demande si le chemin pour aller à la prochaine intersection de la route A est plus court en partant de l’intersection précédente de A et en allant tout droit, ou en partant de l’intersection précédente de B, en avançant et traversant. On se souvient du chemin le plus court, de son coût, et on fait pareil pour l’intersection opposée. On continue pour chaque section jusqu’à atteindre l’arrivée, et le plus court des deux chemins jusqu’aux deux intersections de l’arrivée est notre chemin optimal !

Pour faire simple, on garde un chemin le plus court sur A et un chemin le plus court sur B, jusqu’à atteindre l’arrivée, où le plus court des deux est le chemin optimal. On sait à présent trouver le chemin le plus court à la main. Si vous disposiez d’assez de temps, de papier et de stylos, vous pourriez trouver le chemin le plus court dans un système routier arbitrairement grand.

Prochaine étape ! Comment représenter le système routier avec des types de données d’Haskell ? Une manière consiste à imaginer les points de départ et d’intersection comme des nœuds d’un graphe qui pointe vers d’autres intersections. Si on imagine que les points de départs pointent l’un vers l’autre via une route de longueur nulle, on voit que chaque intersection (ou nœud) pointe vers le nœud du côté opposé et vers le prochain nœud du même côté. À l’exception des derniers nœuds, qui ne pointent que l’un vers l’autre.

data Node = Node Road Road | EndNode Road
data Road = Road Int Node

Un nœud est soit un nœud normal, avec l’information sur la route qui mène au nœud correspondant de l’autre route et celle sur la route qui amène au nœud suivant, soit un nœud final, qui ne contient que l’information vers le nœud opposé. Une route contient pour information sa longueur et le nœud vers lequel elle pointe. Par exemple, la première partie de la route A serait Road 50 a1 où a1 serait un nœud Node x y, où x et y sont des routes qui pointent vers B1 et A2.

Un autre moyen serait d’utiliser Maybe pour les parties de la route qui pointent vers l’avant. Chaque nœud a une route vers le nœud opposé, mais seuls les nœuds non terminaux ont une route vers le prochain nœud.

data Node = Node Road (Maybe Road)
data Road = Road Int Node

C’est une manière correcte de représenter le système routier en Haskell et on pourrait certainement résoudre le problème avec, mais on pourrait peut-être trouver quelque chose de plus simple ? Si on revient sur notre solution à la main, on n’a jamais vérifié que les longueurs de trois parties de routes à la fois : la partie de la route A, sa partie opposée sur la route B, et la partie C qui relie l’arrivée des deux parties précédentes. Quand on cherchait le plus court chemin vers A1 et B1, on ne se souciait que des longueurs des trois premières parties, qui avaient pour longueur 50, 10 et 30. On appellera cela une section. Ainsi, le système routier qu’on utilise pour l’exemple peut facilement être représenté par quatre sections : 50, 10, 30, 5, 90, 20, 40, 2, 25, and 10, 8, 0.

Il est toujours bon de garder nos types de données aussi simples que possible, mais pas trop simples non plus !

data Section = Section { getA :: Int, getB :: Int, getC :: Int } deriving (Show)
type RoadSystem = [Section]

C’est plutôt parfait ! C’est aussi simple que possible, et je pense que ça suffira amplement pour implémenter notre solution. Section est un simple type de données algébriques qui contient trois entiers pour la longueur des trois parties de route de la section. On introduit également un synonyme de type, nommant RoadSystem une liste de sections.

Notre système routier d’Heathrow à Londres peut être représenté ainsi :

heathrowToLondon :: RoadSystem
heathrowToLondon = [Section 50 10 30, Section 5 90 20, Section 40 2 25, Section 10 8 0]

Tout ce dont on a besoin à présent, c’est d’implémenter la solution qu’on a trouvée précédemment en Haskell. Que devrait-être la déclaration de type de la fonction qui calcule le plus court chemin pour n’importe quel système routier ? Elle devrait prendre un système routier en paramètre, et retourner un chemin. On représentera un chemin sous forme de liste. Introduisons un type Label, qui sera juste une énumération A, B ou C. On fera également un synonyme de type : Path.

data Label = A | B | C deriving (Show)
type Path = [(Label, Int)]

Notre fonction, appelons-la optimalPath, devrait donc avoir pour déclaration de type optimalPath :: RoadSystem -> Path. Si elle est appelée avec le système routier heathrowToLondon, elle doit retourner le chemin suivant :

[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8)]

On va devoir traverser la liste des sections de la gauche vers la droite, et garder de côté le chemin optimal sur A et celui sur B. On va accumuler le meilleur chemin pendant qu’on traverse la liste, de la gauche vers la droite. Est-ce que ça sonne familier ? Ding, ding, ding ! Et oui, c’est un PLI GAUCHE !

Quand on déroulait la solution à la main, il y avait une étape qu’on répétait à chaque fois. Ça impliquait de vérifier les chemins optimaux sur A et B jusqu’ici et la section courante pour produire les nouveaux chemins optimaux sur A et B. Par exemple, au départ, nos chemins optimaux sont [] et [] pour A et B respectivement. On examinait la section Section 50 10 30 et on a conclu que le nouveau chemin optimal jusqu’à A1 était [(B,10),(C,30)] et que le chemin optimal jusqu’à B1 était [(B,10)]. Si vous regardez cette étape comme une fonction, elle prend une paire de chemins et une section, et produit une nouvelle paire de chemins. Le type est (Path, Path) -> Section -> (Path, Path). Implémentons directement cette fonction, elle sera forcément utile.

roadStep :: (Path, Path) -> Section -> (Path, Path)
roadStep (pathA, pathB) (Section a b c) =
    let priceA = sum $ map snd pathA
        priceB = sum $ map snd pathB
        forwardPriceToA = priceA + a
        crossPriceToA = priceB + b + c
        forwardPriceToB = priceB + b
        crossPriceToB = priceA + a + c
        newPathToA = if forwardPriceToA <= crossPriceToA
                        then (A,a):pathA
                        else (C,c):(B,b):pathB
        newPathToB = if forwardPriceToB <= crossPriceToB
                        then (B,b):pathB
                        else (C,c):(A,a):pathA
    in  (newPathToA, newPathToB)

Que se passe-t-il là ? D’abord, il faut calculer le temps optimal sur la route A en se basant sur le précédent temps optimal sur A, et de même pour B. On fait sum $ map snd pathA, donc si pathA est quelque chose comme [(A,100),(C,20)], priceA devient 120. forwardPriceToA est le temps optimal pour aller à la prochaine intersection de A en venant de la précédente intersection de A. Il est égal au meilleur temps jusqu’au précédent A, plus la longueur de la partie A de la section courante. crossPriceToA est le temps optimal pour aller au prochain A en venant du précédent B et en traversant. Il est égal au meilleur temps jusqu’au précédent B, plus la longueur B de la section, plus la longueur C de la section. On détermine forwardPriceToB et crossPriceToB de manière analogue.

À présent qu’on connaît le meilleur chemin jusqu’à A et B, il ne nous reste plus qu’à trouver les nouveaux chemins jusqu’à A et B. S’il est moins cher d’aller à A en avançant simplement, on définit newPathToA comme (A, a):pathA. On prépose simplement le Label A et la longueur de la section a au chemin optimal jusqu’au point A précédent. En gros, on dit que le meilleur chemin jusqu’à la prochaine intersection sur A est le meilleur chemin jusqu’à la précédente intersection sur A, suivie par la section en avant sur A. Souvenez-vous qu’A n’est qu’une étiquette, alors que a a pour type Int. Pourquoi est-ce qu’on prépose plutôt que de faire pathA ++ [(A, a)] ? Eh bien, ajouter un élément en début de liste (aussi appelé conser) est bien plus rapide que de l’ajouter à la fin. Cela implique que notre chemin sera à l’envers une fois qu’on aura plié la liste avec cette fonction, mais il sera simple de le renverser plus tard. S’il est moins cher d’aller à la prochaine intersection sur A en avançant sur B puis en traversant, alors newPathToA est le chemin jusqu’à la précédente intersection sur B, suivie d’une section en avant sur B et d’une section traversante. On fait de même pour newPathToB, à l’exception que tout est dans l’autre sens.

Finalement, on retourne newPathToA et newPathToB sous forme de paire.

Testons cette fonction sur la première section d’heathrowToLondon. Puisque c’est la première section, les paramètres contenant les meilleurs chemins jusqu’à l’intersection précédente sur A et sur B sera une paire de listes vides.

ghci> roadStep ([], []) (head heathrowToLondon)
([(C,30),(B,10)],[(B,10)])

Souvenez-vous, les chemins sont renversés, lisez-les donc de la droite vers la gauche. Ici, on peut lire que le meilleur chemin jusqu’au prochain A consiste à avancer sur B puis à traverser, et le meilleur chemin jusqu’au prochain B consiste à avancer directement sur B.

Maintenant qu’on a une fonction qui prend une paire de chemins et une section et produit un nouveau chemin optimal, on peut simplement plier sur une liste de sections. roadStep sera appelée avec ([], []) et la première section, et retournera une paire de chemins optimaux pour cette section. Puis, elle sera appelée avec cette paire de chemins et la prochaine section, et ainsi de suite. Quand on a traversé toutes les sections, il nous reste une paire de chemins optimaux, et le plus court des deux est notre réponse. Avec ceci en tête, on peut implémenter optimalPath.

optimalPath :: RoadSystem -> Path
optimalPath roadSystem =
    let (bestAPath, bestBPath) = foldl roadStep ([],[]) roadSystem
    in  if sum (map snd bestAPath) <= sum (map snd bestBPath)
            then reverse bestAPath
            else reverse bestBPath

On plie depuis la gauche roadSystem (souvenez-vous, c’est une liste de sections) avec pour accumulateur initial une paire de chemins vides. Le résultat de ce pli est une paire de chemins, qu’on filtre par motif pour obtenir les chemins. Puis, on regarde lequel est le plus rapide, et on retourne celui-ci. Avant de le retourner, on le renverse, parce que les chemins étaient jusqu’alors renversés parce qu’on avait choisi de conser plutôt que de postposer.

Testons cela !

ghci> optimalPath heathrowToLondon
[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8),(C,0)]

C’est le bon résultat ! Génial ! Il diffère légèrement de celui auquel on s’attendait, parce qu’il y a une étape (C, 0) à la fin, qui signifie qu’on traverse la route à son arrivée à Londres, mais comme cette traversée n’a aucun coût, le résultat reste valide.

On a la fonction qui trouve le chemin optimal, il ne nous reste plus qu’à lire une représentation littérale d’un système routier de l’entrée standard, le convertir en un type RoadSystem, lancer notre fonction optimalPath dessus, et afficher le chemin.

D’abord, créons une fonction qui prend une liste et la découpe en groupes de même taille. On va l’appeler groupsOf. Pour le paramètre [1..10], groupsOf 3 devrait retourner [[1,2,3],[4,5,6],[7,8,9],[10]].

groupsOf :: Int -> [a] -> [[a]]
groupsOf 0 _ = undefined
groupsOf _ [] = []
groupsOf n xs = take n xs : groupsOf n (drop n xs)

Une fonction récursive standard. Pour un xs valant [1..10] et un n égal à 3, ceci est égal à [1,2,3] : groupsOf 3 [4,5,6,7,8,9,10]. Quand la récursivité s’achève, on a notre liste en groupes de trois éléments. Et voici notre fonction main, qui lit l’entrée standard, crée un RoadSystem et affiche le chemin le plus court.

import Data.List

main = do
    contents <- getContents
    let threes = groupsOf 3 (map read $ lines contents)
        roadSystem = map (\[a,b,c] -> Section a b c) threes
        path = optimalPath roadSystem
        pathString = concat $ map (show . fst) path
        pathPrice = sum $ map snd path
    putStrLn $ "The best path to take is: " ++ pathString
    putStrLn $ "The price is: " ++ show pathPrice

D’abord, on récupère le contenu de l’entrée standard. Puis, on appelle lines sur ce contenu pour convertir quelque chose comme "50\n10\n30\n… en ["50","10","30"… et ensuite, on mappe read là-dessus pour obtenir une liste de nombres. On appelle groupsOf 3 sur cette liste pour la changer en une liste de listes de longueur 3. On mappe la lambda (\[a,b,c] -> Section a b c) sur cette liste de listes. Comme vous le voyez, la lambda prend une liste de longueur 3, et la transforme en une section. Donc roadSystem est à présent notre système routier et a un type correct, c’est-à-dire RoadSystem (ou [Section]). On appelle optimalPath avec ça et on obtient le chemin optimal et son coût dans une représentation textuelle agréable qu’on affiche.

Enregistrons le texte suivant :

50
10
30
5
90
20
40
2
25
10
8
0

dans un fichier paths.txt et donnons-le à notre programme.

$ cat paths.txt | runhaskell heathrow.hs
The best path to take is: BCACBBC
The price is: 75

Ça fonctionne à merveille ! Vous pouvez utiliser vos connaissances du module Data.Random pour générer un système routier plus long, que vous pouvez donner à la fonction qu’on a écrite. Si vous obtenez un dépassement de pile, essayez de remplacer foldl par foldl', sa version stricte.