Les fonctions Haskell peuvent prendre d’autres fonctions en paramètres, et retourner des fonctions en valeur de retour. Une fonction capable d’une de ces deux choses est dite d’ordre supérieur. Les fonctions d’ordre supérieur ne sont pas qu’une partie de l’expérience Haskell, elles sont l’expérience Haskell. Elles s’avèrent indispensable pour définir ce que les choses sont plutôt que des étapes qui changent un état et bouclent. Elles sont un moyen très puissant de résoudre des problèmes et de réflexion sur les programmes.

Fonctions curryfiées

En Haskell, toutes les fonctions ne prennent en fait qu’un unique paramètre. Comment avons-nous pu définir des fonctions qui en prenaient plus d’un alors ? Eh bien, grâce à un détail astucieux ! Toutes nos fonctions qui acceptaient plusieurs paramètres jusqu’à présent étaient des fonctions curryfiées. Qu’est-ce que cela signifie ? Vous comprendrez mieux avec un exemple. Prenons cette bonne vieille fonction max. Elle a l’air de prendre deux paramètres, et de retourner le plus grand des deux. Faire max 4 5 crée une fonction qui prend un paramètre, et retourne soit 4, soit ce paramètre. On applique alors cette fonction à la valeur 5 pour produire le résultat attendu. On ne dirait pas comme ça, mais c’est en fait assez cool. Les deux appels suivants sont ainsi équivalents :

ghci> max 4 5
5
ghci> (max 4) 5
5

Mettre une espace entre deux choses consiste à appliquer une fonction. L’espace est en quelque sorte un opérateur, et il a la plus grande précédence. Examinons le type de max. C’est max :: (Ord a) => a -> a -> a. On peut aussi écrire ceci : max :: (Ord a) => a -> (a -> a). Et le lire ainsi : max prend un a et retourne (c’est le premier ->)) une fonction qui prend un a et retourne un a. C’est pourquoi le type de retour et les paramètres d’une fonction sont séparés par des flèches.

En quoi cela nous aide-t-il ? Pour faire simple, si on appelle une fonction avec trop peu de paramètres, on obtient une fonction appliquée partiellement, c’est à dire une fonction qui prend autant de paramètres qu’on en a oubliés. Utiliser l’application partielle (appeler une fonction avec trop peu de paramètres) est un moyen gracieux de créer des fonctions à la volée et de les passer à d’autres fonctions pour qu’elle les complète avec d’autres données.

Regardons cette fonction violemment simple :

multThree :: (Num a) => a -> a -> a -> a
multThree x y z = x * y * z

Que se passe-t-il vraiment quand on fait multThree 3 5 9 ou ((multThree 3) 5) 9 ? D’abord, 3 est appliqué à multThree, car ils sont séparés par une espace. Cela crée une fonction qui prend un paramètre et retourne une fonction. Ensuite, 5 est appliqué à cette nouvelle fonction, ce qui crée une fonction qui prend un paramètre et le multiplie par 15. 9 est appliqué à cette dernière et le résultat est un truc comme 135. Rappelez-vous que le type de cette fonction peut être écrit comme multThree :: (Num a) => a -> (a -> (a -> a)). La chose avant -> est l’unique paramètre de la fonction, et la chose après est son unique type retourné. Donc, notre fonction prend un a et retourne une fonction qui a pour type (Num a) => a -> (a -> a). De façon similaire, cette fonction prend un a et retourne une fonction qui a pour type (Num a) => a -> a. Et cette fonction, prend un a et retourne un a. Regardez ça :

ghci> let multTwoWithNine = multThree 9
ghci> multTwoWithNine 2 3
54
ghci> let multWithEighteen = multTwoWithNine 2
ghci> multWithEighteen 10
180

En appelant des fonctions avec trop peu de paramètres, en quelque sorte, on crée de nouvelles fonctions à la volée. Comment créer une fonction qui prend un nombre, et le compare à 100 ? Comme ça :

compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred x = compare 100 x

Si on l’appelle avec 99, elle retourne GT. Simple. Remarquez-vous le x tout à droite des deux côtés de l’équation ? Réfléchissons à présent à ce que compare 100 retourne. Cela retourne une fonction qui prend un nombre, et le compare à 100. Ouah ! Est-ce que ce n’était pas la fonction qu’on voulait ? On devrait réécrire cela :

reWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred = compare 100

La déclaration de type est inchangée, car compare 100 retourne bien une fonction. compare a pour type (Ord a) => a -> (a -> Ordering) et l’appeler avec la valeur 100 retourne un (Num a, Ord a) => a -> Ordering). Une classe de contrainte additionnelle s’est insinuée ici parce que 100 est un élément de la classe Num.

Les fonctions infixes peuvent aussi être appliquées partiellement à l’aide de sections. Sectionner une fonction infixe revient à l’entourer de parenthèses et à lui fournir un paramètre sur l’un de ses côtés. Cela crée une fonction qui attend l’autre paramètre et l’applique du côté où il lui manquait une opérande. Une fonction insultante de trivialité :

divideByTen :: (Floating a) => a -> a
divideByTen = (/10)

Appeler, disons, divideByTen 200 est équivalent à faire 200 / 10, ce qui est aussi équivalent à (/10) 200. Maintenant, une fonction qui vérifie si un caractère est en majuscule :

isUpperAlphanum :: Char -> Bool
isUpperAlphanum = (`elem` ['A'..'Z'])

La seule chose spéciale à propos des sections, c’est avec -. Par définition des sections, (-4) devrait être la fonction qui attend un nombre, et lui soustrait 4. Cependant, par habitude, (-4) signifie la valeur moins quatre. Pour créer une fonction qui soustrait 4 du nombre en paramètre, appliquez plutôt partiellement la fonction subtract ainsi : (subtract 4).

Que se passe-t-il si on tape multThree 3 4 directement dans GHCi sans la lier avec un let ou la passer à une autre fonction ?

ghci> multThree 3 4
<interactive>:1:0:
    No instance for (Show (t -> t))
      arising from a use of `print' at <interactive>:1:0-12
    Possible fix: add an instance declaration for (Show (t -> t))
    In the expression: print it
    In a 'do' expression: print it

GHCi nous dit que l’expression produite est une fonction de type a -> a mais qu’il ne sait pas afficher cela à l’écran. Les fonctions ne sont pas des instances de la classe Show, donc elles n’ont pas de représentation littérale. Quand on entre 1 + 1 dans GHCi, il calcule d’abord la valeur 2 puis appelle show sur 2 pour obtenir une représentation textuelle de ce nombre. La représentation de 2 est "2", et c’est ce qu’il nous affiche.

À l’ordre du jour : de l’ordre supérieur

Les fonctions peuvent prendre des fonctions en paramètres et retourner des fonctions. Pour illustrer cela, nous allons créer une fonction qui prend une fonction en paramètre, et l’applique deux fois à quelque chose !

applyTwice :: (a -> a) -> a -> a
applyTwice f x = f (f x)

D’abord, remarquez la déclaration de type. Avant, on n’avait pas besoin de parenthèses, parce que -> est naturellement associatif à droite. Ici, au contraire, elles sont obligatoires. Elles indiquent que le premier paramètre est une fonction qui prend quelque chose et retourne une chose du même type. Le second paramètre est quelque chose également de ce type, et la valeur retournée est elle aussi de ce type. On pourrait lire cette déclaration de type de manière curryfiée, mais pour ne pas se prendre trop la tête, disons juste qu’elle prend deux paramètres, et retourne une chose. Le premier paramètre est une fonction (de type a -> a) et le second est du même type a. La fonction peut très bien être de type Int -> Int ou String -> String ou quoi que ce soit. Mais alors, le second paramètre doit être du type correspondant.

Le corps de la fonction est plutôt simple. On utilise le paramètre f comme une fonction, on applique cette fonction à x en les séparant par une espace, puis on applique f au résultat une nouvelle fois. Jouons un peu avec la fonction :

ghci> applyTwice (+3) 10
16
ghci> applyTwice (++ " HAHA") "HEY"
"HEY HAHA HAHA"
ghci> applyTwice ("HAHA " ++) "HEY"
"HAHA HAHA HEY"
ghci> applyTwice (multThree 2 2) 9
144
ghci> applyTwice (3:) [1]
[3,3,1]

L’application partielle de fonction est évidemment géniale et très utile. Si notre fonction a besoin d’une fonction qui prend un paramètre, on peut lui passer une autre fonction, qu’on aura partiellement appliquée jusqu’à ce qu’il ne lui manque plus qu’un paramètre.

Maintenant, nous allons profiter de la programmation d’ordre supérieur pour implémenter une fonction très utile de la bibliothèque standard. Elle s’appelle zipWith. Elle prend une fonction, et deux listes, et zippe les deux listes à l’aide de la fonction, en l’appliquant aux éléments correspondants. Voici une implémentation :

zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith' _ [] _ = []
zipWith' _ _ [] = []
zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys

Regardez la déclaration de type. Le premier paramètre est une fonction qui attend deux choses pour en produire une troisième. Elles n’ont pas à avoir le même type, mais elles le peuvent tout de même. Les deuxième et troisième paramètres sont des listes. Le résultat est aussi une liste. La première liste est une liste de a, parce que la fonction de jointure attend un a en premier argument. La deuxième doit être une liste de b parce que la fonction de jointure attend un b ensuite. Le résultat est une liste de c. Si la déclaration de type d’une fonction dit qu’elle accepte un a -> b -> c, alors elle peut accepter une fonction de type a -> a -> a, mais pas l’inverse ! Rappelez-vous que quand vous écrivez des fonctions, notamment d’ordre supérieur, et que vous n’êtes pas certain du type, vous pouvez juste omettre la déclaration de type et vérifier ce qu’Haskell a inféré avec :t.

L’action dans la fonction est assez proche du zip normal. Les conditions de base sont les mêmes, seulement il y a un argument de plus, la fonction de jointure, mais puisqu’on ne va pas s’en servir ici, on met juste un _. Le corps de la fonction pour le dernier motif est également similaire à zip, seulement à la place de faire (x, y), elle fait f x y. Une même fonction d’ordre supérieur peut être utilisée pour une multitude de différentes tâches si elle est assez générale. Voici une petite démonstration de toutes les différentes choses que zipWith' peut faire :

ghci> zipWith' (+) [4,2,5,6] [2,6,2,3]
[6,8,7,9]
ghci> zipWith' max [6,3,2,1] [7,3,1,5]
[7,3,2,5]
ghci> zipWith' (++) ["foo ", "bar ", "baz "] ["fighters", "hoppers", "aldrin"]
["foo fighters","bar hoppers","baz aldrin"]
ghci> zipWith' (*) (replicate 5 2) [1..]
[2,4,6,8,10]
ghci> zipWith' (zipWith' (*)) [[1,2,3],[3,5,6],[2,3,4]] [[3,2,2],[3,4,5],[5,4,3]]
[[3,4,6],[9,20,30],[10,12,12]]

Comme vous le voyez, une même fonction d’ordre supérieur peut être utilisée très flexiblement à plusieurs usages. La programmation impérative utilise généralement des trucs comme des boucles for, des boucles while, des affectations de variables, des vérifications de l’état courant, etc. pour arriver à un comportement, puis l’encapsule dans une interface, comme une fonction. La programmation fonctionnelle utilise des fonctions d’ordre supérieur pour abstraire des motifs récurrents, comme examiner deux listes paire à paire et faire quelque chose avec ces paires, ou récupérer un ensemble de solutions et éliminer celles qui ne vous intéressent pas.

Nous allons encore implémenter une fonction de la bibliothèque standard, flip. Elle prend une fonction et retourne une fonction qui est comme la fonction initiale, mais dont les deux premiers arguments ont échangé leur place. On peut l’implémenter ainsi :

flip' :: (a -> b -> c) -> (b -> a -> c)
flip' f = g
    where g x y = f y x

En lisant la déclaration de type, on voit qu’elle prend une fonction qui prend un a puis un b et retourne une fonction qui prend un b puis un a. Mais puisque les fonctions sont curryfiées par défaut, la deuxième paire de parenthèses ne sert en fait à rien, vu que -> est associatif à droite par défaut. (a -> b -> c) -> (b -> a -> c) est la même chose que (a -> b -> c) -> (b -> (a -> c)), qui est aussi la même chose que (a -> b -> c) -> b -> a -> c. On écrit que g x y = f y x. Si c’est le cas, alors f y x = g x y n’est-ce pas ? Avec cela en tête, on peut définir la fonction encore plus simplement.

flip' :: (a -> b -> c) -> b -> a -> c
flip' f y x = f x y

Ici, on profite du fait que les fonctions soient curryfiées. Quand on appelle flip' f sans les paramètres y et x, elle retourne une f qui prend ces deux paramètres et appelle l’originale avec les arguments dans l’ordre inverse. Bien que les fonctions retournées ainsi sont généralement passées à d’autres fonctions, on peut se servir de la curryfication lorsqu’on écrit des fonctions d’ordre supérieur en réfléchissant à ce que leur résultat serait si elles étaient appliquées entièrement.

ghci> flip' zip [1,2,3,4,5] "hello"
[('h',1),('e',2),('l',3),('l',4),('o',5)]
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]
[5,4,3,2,1]

Maps et filtres

map prend une fonction et une liste, et applique la fonction à tous les éléments de la liste, résultant en une nouvelle liste. Regardons sa signature et sa définition.

map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs

La signature dit qu’elle prend une fonction de a vers b, une liste de a, et retourne une liste de b. Il est intéressant de voir que rien qu’en regardant la signature d’une fonction, vous pouvez parfois dire exactement ce qu’elle fait. map est une de ces fonctions d’ordre supérieur extrèmement utile qui peut être utilisée de milliers de façons différentes. La voici en action :

ghci> map (+3) [1,5,3,1,6]
[4,8,6,4,9]
ghci> map (++ "!") ["BIFF", "BANG", "POW"]
["BIFF!","BANG!","POW!"]
ghci> map (replicate 3) [3..6]
[[3,3,3],[4,4,4],[5,5,5],[6,6,6]]
ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]]
[[1,4],[9,16,25,36],[49,64]]
ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)]
[1,3,6,2,2]

Vous avez probablement remarqué que chacun de ces exemples aurait pu être réalisé à l’aide de listes en compréhension. map (+3) [1, 5, 3, 1, 6] est équivalent à [x+3 | x <- [1, 5, 3, 1, 6]]. Cependant, utiliser map est bien plus lisible dans certains cas où vous ne faites qu’appliquer une fonction à chaque élément de la liste, surtout quand vous mappez un map auquel cas les crochets s’entassent de manière déplaisante.

filter est une fonction qui prend un prédicat (un prédicat est une fonction qui dit si quelque chose est vrai ou faux, une fonction qui retourne une valeur booléenne) et une liste, et retourne la liste des éléments qui satisfont le prédicat. La signature et l’implémentation :

filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs)
    | p x       = x : filter p xs
    | otherwise = filter p xs

Plutôt simple. Si p x vaut True, l’élément est inclus dans la nouvelle liste. Sinon, il reste dehors. Quelques exemples d’utilisation :

ghci> filter (>3) [1,5,3,2,1,6,4,3,2,1]
[5,6,4]
ghci> filter (==3) [1,2,3,4,5]
[3]
ghci> filter even [1..10]
[2,4,6,8,10]
ghci> let notNull x = not (null x) in filter notNull [[1,2,3],[],[3,4,5],[2,2],[],[],[]]
[[1,2,3],[3,4,5],[2,2]]
ghci> filter (`elem` ['a'..'z']) "u LaUgH aT mE BeCaUsE I aM diFfeRent"
"uagameasadifeent"
ghci> filter (`elem` ['A'..'Z']) "i lauGh At You BecAuse u r aLL the Same"
"GAYBALLS"

Tout ceci pourrait aussi être fait à base de listes en compréhension avec des prédicats. Il n’y a pas de règle privilégiant l’utilisation de map et filter à celle des listes en compréhension, vous devez juste décider de ce qui est plus lisible en fonction du code et du contexte. L’équivalent pour filter de l’application de plusieurs prédicats dans une liste en compréhension est soit en filtrant plusieurs fois d’affilée, soit en fusionnant des prédicats à l’aide de &&.

Vous souvenez-vous de la fonction quicksort du chapitre précédent ? Nous avions utilisé des listes en compréhension pour filtrer les éléments plus petits que le pivot. On peut faire de même avec filter :

quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
    let smallerSorted = quicksort (filter (<=x) xs)
        biggerSorted = quicksort (filter (>x) xs)
    in  smallerSorted ++ [x] ++ biggerSorted

Mapper et filtrer sont le marteau et le clou de la boîte à outils de tout programmeur fonctionnel. Bon, il importe peut que vous utilisiez plutôt map et filter que des listes en compréhension. Souvenez-vous comment nous avions résolu le problème de trouver les triangles rectangles avec un certain périmètre. En programmation impérative, nous aurions imbriqué trois boucles, dans lequelles nous aurions testé si la combinaison courante correspondait à un triangle rectangle et avait le bon périmètre, auquel cas nous en aurions fait quelque chose comme l’afficher à l’écran. En programmation fonctionnelle, ceci est effectué par mappage et filtrage. Vous créez une fonction qui prend une valeur et produit un résultat. Vous mappez cette fonction sur une liste de valeurs, puis vous filtrez la liste résultante pour obtenir les résultats qui satisfont votre recherche. Et grâce à la paresse d’Haskell, même si vous mappez et filtrez sur une liste plusieurs fois, la liste ne sera traversée qu’une seule fois.

Trouvons le plus grand entier inférieur à 100 000 qui soit divisible par 3 829. Pour cela, filtrons un ensemble de solutions pour lesquelles on sait que le résultat s’y trouve.

largestDivisible :: (Integral a) => a
largestDivisible = head (filter p [100000,99999..])
    where p x = x `mod` 3829 == 0

On crée d’abord une liste de tous les entiers inférieurs à 100 000 en décroissant. Puis, on la filtre par un prédicat, et puisque les nombres sont en ordre décroissant, le plus grand d’entre eux sera simplement le premier élément de la liste filtrée. On n’a même pas eu besoin d’une liste finie pour démarrer. Encore un signe de la paresse en action. Puisque l’on n’utilise que la tête de la liste filtrée, peu importe qu’elle soit finie ou infinie. L’évaluation s’arrête dès que la première solution est trouvée.

Maintenant, trouvons la somme de tous les carrés impairs inférieurs à 10 000. Mais d’abord, puisqu’on va l’utiliser dans la solution, introduisons la fonction takeWhile. Elle prend un prédicat et une liste, et parcourt cette liste depuis le début en retournant tous les éléments tant que le prédicat reste vrai. Dès qu’un élément ne satisfait plus le prédicat, elle s’arrête. Si l’on voulait le premier mot d’une chaîne comme "elephants know how to party", on pourrait faire takeWhile (/=' ') "elephants know how to party" et cela retournerait "elephants". Ok. La somme des carrés impairs inférieurs à dix mille. D’abord, on va commencer par mapper (^2) sur la liste infinie [1..]. Ensuite, on va filtrer pour garder les nombres impairs. Puis, on prendra des éléments de cette liste tant qu’ils restent inférieurs à 10 000. Enfin, on va sommer cette liste. On n’a même pas besoin d’une fonction pour ça, une ligne dans GHCi suffit :

ghci> sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
166650

Génial ! On commence avec une donnée initiale (la liste infinie de tous les entiers naturels) et on mappe par dessus, puis on filtre et on coupe jusqu’à avoir ce que l’on désire, et on somme le tout. On aurait pu écrire ceci à l’aide de listes en compréhension :

ghci> sum (takeWhile (<10000) [n^2 | n <- [1..], odd (n^2)])
166650

C’est une question de goût, à vous de choisir la forme que vous préférez. Encore une fois, la paresse d’Haskell rend ceci possible. On peut mapper et filtrer une liste infinie, puisqu’il ne va pas mapper et filtrer directement, il retardera ces actions. C’est seulement quand on demande à Haskell de nous montrer la somme que la fonction sum dit à la fonction takeWhile qu’elle a besoin de cette liste de nombre. takeWhile force le filtrage et le mappage, en demandant des nombres un par un tant qu’il n’en croise pas un plus grand que 10000.

Pour notre prochain problème, on va se confronter aux suites de Collatz. On prend un entier naturel. Si cet entier est pair, on le divise par deux. S’il est impair, on le multiplie par 3 puis on ajoute 1. On prend ce nombre, et on recommence, ce qui produit un nouveau nombre, et ainsi de suite. On obtient donc une chaîne de nombres. On pense que, quel que soit le nombre de départ, la chaîne termine, avec pour valeur 1. Si on prend 13, on obtient la suite : 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. 13 fois 3 plus 1 vaut 40. 40 divisé par 2 vaut 20, etc. On voit que la chaîne contient 10 termes.

Maintenant on cherche à savoir : pour tout nombre de départ compris entre 1 et 100, combien de chaînes ont une longueur supérieure à 15 ? D’abord, on va écrire une fonction qui produit ces chaînes :

chain :: (Integral a) => a -> [a]
chain 1 = [1]
chain n
    | even n =  n:chain (n `div` 2)
    | odd n  =  n:chain (n*3 + 1)

Puisque les chaînes terminent à 1, c’est le cas de base. C’est une fonction récursive assez simple.

ghci> chain 10
[10,5,16,8,4,2,1]
ghci> chain 1
[1]
ghci> chain 30
[30,15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]

Yay ! Ça a l’air de marcher correctement. À présent, la fonction qui nous donne notre réponse :

numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
    where isLong xs = length xs > 15

On mappe la fonction chain sur la liste [1..100] pour obtenir une liste de toutes les chaînes, qui sont elles-même représentées sous forme de listes. Puis, on les filtre avec un prédicat qui vérifie simplement si la longueur est plus grande que 15. Une fois ceci fait, il ne reste plus qu’à compter le nombre de chaînes dans la liste finale.

En utilisant map, on peut faire des trucs comme map (*) [0..], par exemple pour illustrer la curryfication et le fait que les fonctions appliquées partiellement sont de vraies valeurs que l’on peut manipuler et placer dans des listes (par contre, on ne peut pas les transformer en chaînes de caractères). Pour l’instant, on a seulement mappé des fonctions qui attendent un paramètre sur des listes, comme map (*2) [0..] pour obtenir des listes de type (Num a) => [a], mais on peut aussi faire map (*) [0..] sans problème. Ce qui se passe ici, c’est que le nombre dans la liste s’applique à la fonction *, qui a pour type (Num a) => a -> a -> a. Appliquer une fonction sur un paramètre, alors qu’elle en attend deux, retourne une fonction qui attend encore un paramètre. Si l’on mappe * sur [0..], on obtient en retour une liste de fonctions qui attendent chacune un paramètre, donc (Num a) [a -> a]. map (*) [0..] produit une liste comme celle qu’on obtiendrait en écrivant [(0*), (1*), (2*), (3*), (4*), (5*), …].

ghci> let listOfFuns = map (*) [0..]
ghci> (listOfFuns !! 4) 5
20

Demander l’élément d’index 4 de notre liste retourne une fonction équivalente à (4*). Puis on applique cette fonction à 5. Donc c’est comme écrire (4*) 5 ou juste 4 * 5.

Lambdas

Les lambda expressions sont simplement des fonctions anonymes utilisées lorsqu’on a besoin d’une fonction à usage unique. Normalement, on crée une lambda uniquement pour la passer à une fonction d’ordre supérieur. Pour créer une lambda, on écrit un \ (parce que ça ressemble à la lettre grecque lambda si vous le fixez assez longtemps des yeux) puis les paramètres, séparés par des espaces. Après cela vient -> puis le corps de la fonction. On l’entoure généralement de parenthèses, autrement elle s’étend autant que possible vers la droite.

Si vous regardez 10cm plus haut, vous verrez qu’on a utilisé une liaison where dans numLongChains pour créer la fonction isLong, avec pour seul but de passer cette fonction à filter. Au lieu de faire ça, on pourrait utiliser une lambda :

numLongChains :: Int
numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]))

Les lambdas sont des expressions, c’est pourquoi on peut les manipuler comme ça. L’expression (\xs -> length xs > 15) retourne une fonction qui nous dit si la longueur de la liste passée en paramètre est plus grande que 15.

Les personnes n’étant pas habituées à la curryfication et à l’application partielle de fonctions utilisent souvent des lambdas là où ils n’en ont en fait pas besoin. Par exemple, les expressions map (+3) [1, 6, 3, 2] et map (\x -> x + 3) [1, 6, 3, 2] sont équivalentes puisque (+3) tout comme (\x -> x + 3) renvoient toutes les deux le nombre passé en paramètre plus 3. Il est inutile de vous préciser que créer une lambda dans ce cas est stupide puisque l’application partielle est bien plus lisible.

Comme les autres fonctions, les lambdas peuvent prendre plusieurs paramètres.

ghci> zipWith (\a b -> (a * 30 + 3) / b) [5,4,3,2,1] [1,2,3,4,5]
[153.0,61.5,31.0,15.75,6.6]

Et comme les fonctions, vous pouvez filtrer par motif dans les lambdas. La seule différence, c’est que vous ne pouvez pas définir plusieurs motifs pour un paramètre, comme par exemple créer un motif [] et un (x:xs) pour le même paramètre, et avoir les valeurs parcourir les différents motifs. Si un filtrage par motif échoue dans une lambda, une erreur d’exécution a lieu, donc faites attention en filtrant dans les lambdas.

ghci> map (\(a,b) -> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)]
[3,8,9,8,7]

Les lambdas sont habituellement entourées de parenthèses à moins qu’on veuille qu’elles s’étendent le plus possible à droite. Voilà quelque chose d’intéressant : vu la façon dont sont curryfiées les fonctions par défaut, ces deux codes sont équivalents :

addThree :: (Num a) => a -> a -> a -> a
addThree x y z = x + y + z

addThree :: (Num a) => a -> a -> a -> a
addThree = \x -> \y -> \z -> x + y + z

Si on définit une fonction ainsi, il devient évident que la signature doit avoir cette forme. Il y a trois -> dans le type et dans l’équation. Mais bien sûr, la première façon d’écrire est bien plus lisible, la seconde ne sert qu’à illustrer la curryfication.

Cependant, cette notation s’avère parfois pratique. Je trouve la fonction flip plus lisible définie ainsi :

flip' :: (a -> b -> c) -> b -> a -> c
flip' f = \x y -> f y x

Bien que ce soit comme écrire flip' f x y = f y x, on fait apparaître clairement que ce sera utilisé pour créer une nouvelle fonction la plupart du temps. L’utilisation la plus classique de flip consiste à appeler la fonction avec juste une autre fonction, et de passer le résultat à un map ou un filter. Utilisez donc les lambdas lorsque vous voulez rendre explicite le fait que cette fonction est généralement appliquée partiellement avant d’être passée à une autre comme paramètre.

Plie mais ne rompt pas

À l’époque où nous faisions de la récursivité, nous avions repéré un thème récurrent dans nos fonctions récursives qui opéraient sur des listes. Nous introduisions un motif x:xs et nous faisions quelque chose avec la tête et quelque chose avec la queue. Il s’avère que c’est un motif très commun, donc il existe quelques fonctions très utiles qui l’encapsulent. Ces fonctions sont appelées des folds (NDT : des plis). Elles sont un peu comme la fonction map, seulement qu’elles réduisent une liste à une valeur unique.

Un fold prend une fonction binaire, une valeur de départ (que j’aime appeler l’accumulateur) et une liste à plier. La fonction binaire prend deux paramètres. Elle est appelée avec l’accumulateur en première ou deuxième position, et le premier ou le dernier élément de la liste comme autre paramètre, et produit un nouvel accumulateur. La fonction est appelée à nouveau avec le nouvel accumulateur et la nouvelle extrémité de la queue, et ainsi de suite. Une fois qu’on a traversé toute la liste, seul l’accumulateur reste, c’est la valeur à laquelle on a réduit la liste.

D’abord, regardons la fonction foldl, aussi appelée left fold (pli à gauche). Elle plie la liste en partant de la gauche. La fonction binaire est appelée avec la valeur de départ de l’accumulateur et la tête de liste. Cela produit un nouvel accumulateur, et la fonction est à nouveau appelée sur cette valeur et le prochain élément de la liste, etc.

Implémentons sum à nouveau, mais cette fois, utilisons un fold plutôt qu’une récursivité explicite.

sum' :: (Num a) => [a] -> a
sum' xs = foldl (\acc x -> acc + x) 0 xs

Un, deux, trois, test :

ghci> sum' [3,5,2,1]
11

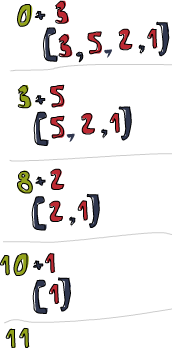
Regardons de près comment ce pli se déroule. \acc x -> acc + x est la fonction binaire. 0 est la valeur de départ et xs la liste à plier. D’abord, 0 est utilisé pour acc et 3 pour x. 0 + 3 retourne 3 et devient, pour ainsi dire, le nouvel accumulateur. Ensuite, 3 est utilisé comme accumulateur, et l’élément courant, 5, résultant en un 8 comme nouvel accumulateur. Encore en avant, 8 est l’accumulateur, 2 la valeur courante, le nouvel accumulateur est donc 10. Utilisé avec la valeur courante 1, il produit 11. Bravo, vous venez d’achever votre premier pli !

Le diagramme professionnel sur la gauche illustre la façon dont le pli se déroule, étape par étape (jour après jour !). Le nombre vert kaki est l’accumulateur. Vous pouvez voir comme la liste est consommée par la gauche par l’accumulateur. Om nom nom nom ! (NDT : “Miam miam miam !”) Si on prend en compte le fait que les fonctions sont curryfiées, on peut écrire cette implémentation encore plus rapidement :

sum' :: (Num a) => [a] -> a
sum' = foldl (+) 0

La lambda (\acc x -> acc + x) est équivalente à (+). On peut omettre le xs à la fin parce que foldl (+) 0 retourne une fonction qui attend une liste. En général, lorsque vous avec une fonction foo a = bar b a, vous pouvez réécrire foo = bar b, grâce à la curryfication.

Bon, implémentons une autre fonction avec un pli à gauche avant de passer aux plis à droite. Je suis sûr que vous savez tous qu’elem vérifie si une valeur fait partie d’une liste, donc je ne vais pas vous le rappeler (oups, je viens de le faire !). Implémentons-là avec un pli à gauche.

elem' :: (Eq a) => a -> [a] -> Bool
elem' y ys = foldl (\acc x -> if x == y then True else acc) False ys

Bien, bien, bien, qu’avons-nous là ? La valeur de départ et l’accumulateur sont de type booléen. Le type de l’accumulateur et de l’initialisateur est toujours le même quand on plie. Rappelez-vous en quand vous ne savez plus quoi utiliser comme valeur de départ, ça vous mettra sur la piste. Ici, on commence avec False. Il est logique d’utiliser False comme valeur initiale. On présume que l’élément n’est pas là, tant qu’on n’a pas de preuve de sa présence. Notez que si l’on appelle fold sur une liste vide, on obtient en retour la valeur initiale. Ensuite, on vérifie le premier élément pour savoir si c’est celui que l’on cherche. Si c’est le cas, on passe l’accumulateur à True. Sinon, on ne touche pas à l’accumulateur. S’il était False, il reste à False car on ne vient pas de trouver l’élément. S’il était True, on le laisse aussi.

Le pli à droite, foldr travaille de manière analogue au pli à gauche, mais l’accumulateur consomme les valeurs en partant de la droite. Aussi, la fonction binaire du pli gauche prend l’accumulateur en premier paramètre, et la valeur courante en second (\acc x -> …), celle du pli droit prend la valeur courante en premier et l’accumulateur en second (\x acc -> …). C’est assez logique que le pli à droite ait l’accumulateur à droite, vu qu’il plie depuis la droite.

La valeur de l’accumulateur (et donc le résultat) d’un pli peut être de n’importe quel type. Un nombre, un booléen, ou même une liste. Implémentons la fonction map à l’aide d’un pli à droite. L’accumulateur sera la liste, on va accumuler les valeurs après mappage, élément par élément. De fait, il est évident que l’élément de départ sera une liste vide.

map' :: (a -> b) -> [a] -> [b]
map' f xs = foldr (\x acc -> f x : acc) [] xs

Si l’on mappe (+3) à [1, 2, 3], on attaque la liste par la droite. On prend le dernier élément, 3 et on applique la fonction, résultant en un 6. On le place à l’avant de l’accumulateur, qui était []. 6:[] est [6], et notre nouvel accumulateur. On applique (+3) sur 2, donnant 5 et on le place devant (:) l’accumulateur, l’accumulateur devient [5, 6]. On applique (+3) à 1 et on le place devant l’accumulateur, ce qui donne pour valeur finale [4, 5, 6].

Bien sûr, nous aurions pu implémenter cette fonction avec un pli gauche aussi. Cela serait map' f xs = foldl (\acc x -> acc ++ [f x]) [] xs, mais le problème, c’est que ++ est beaucoup plus coûteux que :, donc généralement, on utilise des plis à droite lorsqu’on construit des nouvelles listes à partir d’une liste.

Si vous renversez une liste, vous pouvez faire un pli droit sur une liste comme vous auriez fait un pli gauche sur la liste originale, et vice versa. Parfois, vous n’avez même pas besoin de ça. La fonction sum peut être implémentée aussi bien avec un pli à gauche qu’à droite. Une des grosses différences est que les plis à droite fonctionnent sur des listes infinies, alors que les plis à gauche, non ! Pour mettre cela au clair, si vous prenez un endroit d’une liste infinie et que vous vous mettez à plier depuis la droite depuis celui-ci, vous finirez par atteindre le début de la liste. Par contre, si vous vous placez à un endroit d’une liste infinie, et que vous commencez à plier depuis la gauche vers la droite, vous n’atteindrez jamais la fin !

Les plis peuvent être utilisés pour implémenter n’importe quelle fonction qui traverse une liste une fois, élément par élément, et retourne quoi que ce soit basé là-dessus. Si jamais vous voulez parcourir une liste pour retourner quelque chose, vous aurez besoin d’un pli. C’est pourquoi les plis sont, avec les maps et les filtres, un des types les plus utiles en programmation fonctionnelle.

Les fonctions foldl1 et foldr1 fonctionnent quasiment comme foldl et foldr, mais n’ont pas besoin d’une valeur de départ. Elles considèrent que le premier (ou le dernier respectivement) élément de la liste est la valeur de départ, et commencent à plier à partir de l’élément suivant. Avec cela en tête, la fonction sum peut être implémentée : sum = foldl1 (+). Puisqu’elles dépendent du fait que les listes qu’elles essaient de plier aient au moins un élément, elles peuvent provoquer des erreurs à l’exécution si on les appelle sur des listes vides. foldl et foldr, d’un autre côté, fonctionnent bien sur des listes vides. Quand vous faites un pli, pensez donc à la façon dont il se comporte sur une liste vide. Si la fonction n’a aucun sens pour une liste vide, vous pouvez probablement utiliser foldl1 et foldr1 pour l’implémenter.

Histoire de vous montrer la puissance des plis, on va implémenter un paquet de fonctions de la bibliothèque standard avec eux :

maximum' :: (Ord a) => [a] -> a
maximum' = foldr1 (\x acc -> if x > acc then x else acc)

reverse' :: [a] -> [a]
reverse' = foldl (\acc x -> x : acc) []

product' :: (Num a) => [a] -> a
product' = foldr1 (*)

filter' :: (a -> Bool) -> [a] -> [a]
filter' p = foldr (\x acc -> if p x then x : acc else acc) []

head' :: [a] -> a
head' = foldr1 (\x _ -> x)

last' :: [a] -> a
last' = foldl1 (\_ x -> x)

head est tout de même mieux implémenté par filtrage par motif, mais c’était juste pour l’exemple, que l’on peut y arriver avec des plis. Notre fonction reverse' est à ce titre plutôt astucieuse. On prend pour valeur initiale une liste vide, et on attaque la liste par la gauche en positionnant les éléments rencontrés à l’avant de notre accumulateur. Au final, on a construit la liste renversée. \acc x -> x : acc ressemble assez à la fonction :, mais avec ses paramètres dans l’autre sens. C’est pourquoi, on aurait pu écrire reverse comme foldl (flip (:)) [].

Une autre façon de se représenter les plis à droite et à gauche consiste à se dire : mettons qu’on a un pli à droite et une fonction binaire f, et une valeur initiale z. Si l’on plie à droite la liste [3, 4, 5, 6], on fait en gros cela : f 3 (f 4 (f 5 (f 6 z))). f est appelé avec le dernier élément de la liste et l’accumulateur, cette valeur est donnée comme accumulateur à la prochaine valeur, etc. Si on prend pour f la fonction + et pour accumulateur de départ 0, ça donne 3 + (4 + (5 + (6 + 0))). Ou, avec un + préfixe, (+) 3 ((+) 4 ((+) 5 ((+) 6 0))). De façon similaire, un pli à gauche avec la fonction binaire g et l’accumulateur z est équivalent p g (g (g (g z 3) 4) 5) 6. Si on utilise flip (:) comme fonction binaire, et [] comme accumulateur (de manière à renverser la liste), c’est équivalent à flip (:) (flip (:) (flip (:) (flip (:) [] 3) 4) 5) 6. Et pour sûr, évaluer cette expression renvoie [6, 5, 4, 3].

scanl et scanr sont comme foldl et foldr, mais rapportent tous les résultats intermédiaires de l’accumulateur sous forme d’une liste. Il existe aussi scanl1 et scanr1, analogues à foldl1 et foldr1.

ghci> scanl (+) 0 [3,5,2,1]
[0,3,8,10,11]
ghci> scanr (+) 0 [3,5,2,1]
[11,8,3,1,0]
ghci> scanl1 (\acc x -> if x > acc then x else acc) [3,4,5,3,7,9,2,1]
[3,4,5,5,7,9,9,9]
ghci> scanl (flip (:)) [] [3,2,1]
[[],[3],[2,3],[1,2,3]]

En utilisant un scanl, le résultat final sera dans le dernier élément de la liste retournée, alors que pour un scanr, il sera en tête.

Les scans sont utilisés pour surveiller la progression d’une fonction implémentable comme un pli. Répondons à cette question : Combien d’entiers naturels croissants faut-il pour que la somme de leurs racines carrées dépasse 1000 ? Pour récupérer les racines carrées de tous les entiers naturels, on fait map sqrt [1..]. Maintenant, pour obtenir leur somme, on pourrait faire un pli, mais puisqu’on s’intéresse à la progression de la somme, on va plutôt faire un scan. Une fois le scan fait, on compte juste le nombre de sommes qui sont inférieures à 1000. La première somme sera normalement égale à 1. La deuxième, à 1 plus racine de 2. La troisième à cela plus racine de 3. Si X de ces sommes sont inférieures à 1000, alors il faut X+1 éléments pour dépasser 1000.

sqrtSums :: Int
sqrtSums = length (takeWhile (<1000) (scanl1 (+) (map sqrt [1..]))) + 1

ghci> sqrtSums
131
ghci> sum (map sqrt [1..131])
1005.0942035344083
ghci> sum (map sqrt [1..130])
993.6486803921487

On utilise takeWhile plutôt que filter parce que filter ne peut pas travailler sur des listes infinies. Bien que nous sachions que cette liste est croissante, filter ne le sait pas, donc on utilise takeWhile pour arrêter de scanner dès qu’une somme est plus grande que 1000.

Appliquer des fonctions avec $

Bien, maintenant, découvrons la fonction $, aussi appelée application de fonction. Voyons sa définition :

($) :: (a -> b) -> a -> b
f $ x = f x

De quoi ? Qu’est-ce que c’est que cet opérateur inutile ? C’est juste une application de fonction ! Eh bien, presque, mais pas complètement ! Alors que l’application de fonction habituelle (avec une espace entre deux choses) a une précédence très élevée, la fonction $ a la plus faible précédence. Une application de fonction avec une espace est associative à gauche (f a b c est équivalent à ((f a) b) c), alors qu’avec $ elle est associative à droite.

C’est tout, mais en quoi cela nous aide-t-il ? La plupart du temps, c’est une fonction pratique pour éviter d’écrire des tas de parenthèses. Considérez l’expression sum (map sqrt [1..130]). Puisque $ a une précédence aussi faible, on peut réécrire cette expression sum $ map sqrt [1..130], et éviter de précieuses frappes de clavier ! Quand on rencontre un $, la fonction sur sa gauche s’applique à l’expression sur sa droite. Qu’en est-il de sqrt 3 + 4 + 9 ? Ceci ajoute 9, 4, et la racine de 3. Mais si l’on veut la racine carrée de 3 + 4 + 9, il faut écrire sqrt (3 + 4 + 9), ou avec $, sqrt $ 3 + 4 + 9, car $ a la plus faible précédence de tous les opérateurs. On peut donc voir $ comme le fait d’écrire une parenthèse ouvrante en lieu et place, et d’aller mettre une parenthèse fermante le plus possible à droite de l’expression.

Et sum (filter (> 10) (map (*2) [2..10])) ? Et bien, puisque $ est associatif à droite, f (g (z x)) est égal à f $ g $ z x. On peut donc réécrire l’expression sum $ filter (> 10) $ map (*2) [2..10].

À part pour se débarasser des parenthèses, $ implique aussi que l’on peut traiter l’application de fonction comme n’importe quelle fonction. Ainsi, on peut par exemple mapper l’application de fonction sur une liste de fonctions.

ghci> map ($ 3) [(4+), (10*), (^2), sqrt]
[7.0,30.0,9.0,1.7320508075688772]

Composition de fonctions

En mathématique, la composition de fonctions est définie ainsi : 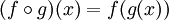, ce qui signifie que deux fonctions produisent une nouvelle fonction qui, lorsqu’elle est appelée avec un paramètre, disons x, est équivalent à l’appel de g sur x, puis l’appel de f sur le résultat.

En Haskell, la composition de fonction est plutôt identique. On utilise la fonction ., définie ainsi :

(.) :: (b -> c) -> (a -> b) -> a -> c
f . g = \x -> f (g x)

Prêtez attention à la déclaration de type. f doit prendre pour paramètre une valeur qui a le même type que la valeur retournée par g. Ainsi, la fonction résultante peut prendre un paramètre du même type que celui attendu par g, et retourner une valeur du même type que celui retourné par f. L’expression negate . (* 3) retourne une fonction qui prend un nombre, le multiplie par 3, et retourne l’opposé.

Une utilisation de la composition de fonctions est de créer des fonctions à la volée pour les passer à d’autre fonctions. Bien sûr, on peut utiliser des lambdas à cet effet, mais souvent, la composition de fonctions est plus claire et concise. Disons qu’on a une liste de nombres, et qu’on veut tous les rendre négatifs. Un moyen de procéder serait de prendre la valeur absolue de chacun d’entre eux, et de renvoyer son opposé :

ghci> map (\x -> negate (abs x)) [5,-3,-6,7,-3,2,-19,24]
[-5,-3,-6,-7,-3,-2,-19,-24]

Remarquez la lambda-expression, comme elle ressemble à une composition de fonctions. Avec la composition, on peut écrire :

ghci> map (negate . abs) [5,-3,-6,7,-3,2,-19,24]
[-5,-3,-6,-7,-3,-2,-19,-24]

Fabuleux ! La composition est associative à droite, donc on peut composer plusieurs fonctions à la fois. L’expression f (g (z x)) est équivalente à (f . g . z) x. Avec ça en tête, on peut transformer :

ghci> map (\xs -> negate (sum (tail xs))) [[1..5],[3..6],[1..7]]
[-14,-15,-27]

en :

ghci> map (negate . sum . tail) [[1..5],[3..6],[1..7]]
[-14,-15,-27]

Mais qu’en est-il des fonctions à plusieurs paramètres ? Pour les utiliser dans de la composition de fonctions, il faut les avoir partiellement appliquées jusqu’à ce qu’elles ne prennent plus qu’un paramètre. sum (replicate 5 (max 6.7 8.9)) peut être réécrit (sum . replicate 5 . max 6.7) 8.9 ou bien sum . replicate 5 . max 6.7 $ 8.9. Ce qui se passe ici : une fonction qui prend la même chose que max 6.7 et applique replicate 5 à celle-ci est créée. Ensuite, une fonction qui prend ça et applique sum est créée. Finalement, cette fonction est appelée avec 8.9. Vous liriez normalement comme cela : prend 8.9 et applique max 6.7, puis applique replicate 5 à ça, et applique sum à ça. Si vous voulez réécrire une expression pleine de parenthèses avec de la composition de fonctions, vous pouvez commencer par mettre le dernier paramètre de la dernière fonction à la suite d’un $, et ensuite composer les appels successifs, en les écrivant sans leur dernier paramètre et en les séparant par des points. Si vous avez replicate 100 (product (map (*3) (zipWith max [1, 2, 3, 4, 5] [4, 5, 6, 7, 8]))), vous pouvez l’écrire replicate 100 . product . map (*3) . zipWith max [1, 2, 3, 4, 5] $ [4, 5, 6, 7, 8]. Si l’expression se terminait par trois parenthèses, la réécriture contiendra probablement trois opérateurs de composition.

Une autre utilisation courante de la composition de fonctions consiste à définir des fonctions avec un style dit sans point (certains disent même sans but !). Prenez par exemple la fonction définie auparavant :

sum' :: (Num a) => [a] -> a
sum' xs = foldl (+) 0 xs

Le xs est exposé à gauche comme à droite. À cause de la curryfication, on peut l’omettre des deux côtés, puisqu’appeler foldl (+) 0 renverra une fonction qui attend une liste. Écrire une fonction comme sum' = foldl (+) 0 est dit dans le style sans point. Comment écrire ceci en style sans point ?

fn x = ceiling (negate (tan (cos (max 50 x))))

On ne peut pas se débarasser du x des deux côtés. Le x du côté du corps de la fonction a des parenthèses après lui. cos (max 50) ne voudrait rien dire. On ne peut pas prendre le cosinus d’une fonction. On peut cependant exprimer fn comme une composition de fonctions :

fn = ceiling . negate . tan . cos . max 50

Excellent ! Souvent, un style sans point est plus lisible et concis, car il vous fait réfléchir en termes de fonctions et de composition de leur résultat, plutôt qu’à la façon dont les données sont transportées d’un endroit à l’autre. Vous pouvez prendre de simples fonctions et utiliser la composition pour les coller et former des fonctions plus complexes. Cependant, souvent, écrire une fonction en style sans point peut être moins lisible parce que la fonction est trop complexe. C’est pourquoi l’on décourage les trop grandes chaînes de composition, bien que je sois coupable d’être fan de composition. Le style préféré consiste à utiliser des liaisons let pour donner des noms aux résultats intermédiaires ou découper le problème en sous-problèmes et ensuite mettre tout en place pour que les fonctions aient du sens pour le lecteur, plutôt que de voir une grosse chaîne de compositions.

Dans la section sur les maps et les filtres, nous avions résolu le problème de trouver la somme des carrés impairs inférieurs à 10000. Voici la solution sous la forme d’une fonction.

oddSquareSum :: Integer
oddSquareSum = sum (takeWhile (<10000) (filter odd (map (^2) [1..])))

Étant un fan de composition, j’aurais probablement écrit :

oddSquareSum :: Integer
oddSquareSum = sum . takeWhile (<10000) . filter odd . map (^2) $ [1..]

Cependant, s’il était possible que quelqu’un doive lire ce code, j’aurais plutôt écrit :

oddSquareSum :: Integer
oddSquareSum =
    let oddSquares = filter odd $ map (^2) [1..]
        belowLimit = takeWhile (<10000) oddSquares
    in  sum belowLimit

Ce code ne gagnerait pas à une compétition de «code golf», mais si quelqu’un devrait le lire, il trouverait certainement cela plus lisible qu’une chaîne de compositions.