Bonjour récursivité !

Nous avons rapidement mentionné la récursivité dans le chapitre précédent. Dans celui-ci, regardons-là de plus près, pourquoi elle est importante en Haskell et comment on peut écrire des solutions concises et élégantes à certains problèmes en réfléchissant récursivement.

Si vous ne savez toujours pas ce qu’est la récursivité, relisez cette phrase. Haha ! Je blague ! La récursivité est en fait une manière de définir des fonctions dans laquelle on utilise la fonction dans sa propre définition. Les définitions mathématiques sont souvent énoncées récursivement. Par exemple, la suite de Fibonacci est définie récursivement. D’abord, on définit les deux premiers nombres de Fibonacci de manière non-récursive. On dit que F(0) = 0 et F(1) = 1, pour dire que le 0ème et le 1er chiffre sont 0 et 1, respectivement. Puis, on dit que pour tout entier naturel, ce nombre de Fibonacci est la somme des deux précédents nombres de Fibonacci. Donc F(n) = F(n-1) + F(n-2). Ainsi, F(3) est F(2) + F(1), qui est (F(1) + F(0)) + F(1). Puisque l’on vient d’atteindre des nombres tous définis non-récursivement, on peut déclarer que F(3) vaut 2. Un ou plusieurs éléments définis non-récursivement dans une définition récursive sont appelés les cas de base de récursivité, et sont importants afin d’assurer que la fonction récursive termine. Sans eux, si F(0) et F(1) n’avaient pas été définis ainsi, on n’obtiendrait jamais de solution car on atteindrait 0, et on continuerait à décroître. Au bout d’un moment, on dirait que F(-2000) est F(-2001) + F(-2002), et on en verrait toujours pas le bout !

La récursivité est importante en Haskell car, contrairement aux langages impératifs, vous faites des calculs en Haskell en définissant ce que les choses sont et non pas comment on les obtient. C’est pour cela qu’il n’y a pas de boucles while et for en Haskell, et à la place, on utilise souvent la récursivité pour déclarer ce qu’est quelque chose.

Maximum de fun

La fonction maximum prend une liste de choses qui peuvent être ordonnées (i.e. des instances de la classe Ord) et retourne la plus grande d’entre elles. Comment implémenteriez-vous ceci de manière impérative ? Vous auriez sûrement une variable qui contiendrait la plus grande valeur rencontrée jusqu’ici, et vous boucleriez à travers les éléments de la liste, remplaçant le maximum courant par un élément s’il s’avère être plus grand. La valeur maximale serait alors le maximum courant une fois arrivé à la fin. Wouah ! Que de mots pour décrire un algorithme aussi simple !

Voyons comment nous le définirions récursivement. Nous aurions d’abord un cas de base, nous disant que le maximum d’une liste singleton est son seul élément. Puis, le maximum d’une liste plus longue est sa tête si elle est plus grande que le maximum de la queue. Sinon, c’est ce dernier qui est le maximum de la liste ! Et voilà ! Implémentons ça en Haskell.

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs

Comme vous le voyez, le filtrage par motif va bien de pair avec la récursivité ! La plupart des langages impératifs ne proposent pas de filtrage par motif, donc vous êtes obligé d’utiliser plein de if else pour tester les cas de base. Ici, on les met simplement dans des motifs. La première condition dit : si la liste est vide, plante ! Raisonnable, après tout quel est le maximum d’une liste vide ? Je ne sais pas. Le deuxième motif est aussi un cas de base. Il dit que pour une liste singleton, il suffit de retourner son unique élément.

Maintenant, le troisième motif est là où se passe l’action. On utilise du filtrage par motif pour séparer la tête et la queue de la liste. C’est un idiome usuel pour faire de la récursivité sur des listes, donc habituez-vous. On utilise une liaison where pour définir maxTail comme le maximum du reste de la liste. Ensuite, on vérifie si la tête est plus grande que le maximum du reste de la liste. Si c’est le cas, la tête est retournée. Sinon, le maximum du reste de la liste est retourné.

Prenons par exemple une liste de nombres et voyons comment cela marche : [2, 5, 1]. Si on appelle maximum' dessus, les deux premiers motifs ne vont pas correspondre. Le troisième marchera, et coupera le 2 du [5, 1]. La clause where veut connaître le maximum de [5, 1], donc on suit cette route. Elle la compare avec succès au troisième motif à nouveau, et [5, 1] est coupé en 5 et [1]. À nouveau, la clause where veut connaître le maximum de [1]. C’est un cas de base, on retourne donc 1. Enfin ! En remontant d’une étape, 5 est comparé au maximum de [1] (qui est 1), et retourne 5. On sait à présent que le maximum de [5, 1] est 5. Une étape plus haut, nous comparions 2 au maximum de [5, 1], qui est 5, et on choisit donc 5.

Une manière encore plus claire d’écrire cette fonction est d’utiliser max. Si vous vous souvenez, max est une fonction qui prend deux nombres et retourne le plus grand d’entre eux. Ici, nous pourrions réécrire maximum' en utilisant max :

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

Comme c’est élégant ! Dans le principe, le maximum d’une liste est le max de son premier élément et du maximum de la queue.

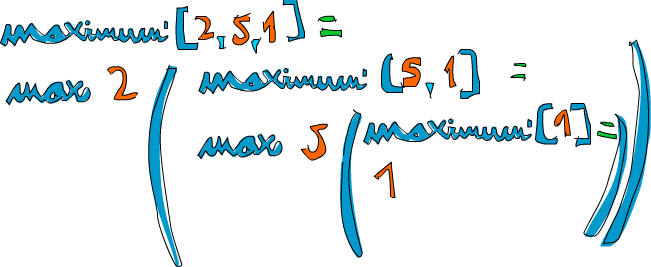
Un peu plus de fonctions récursives

Maintenant que l’on sait penser en termes de récursivité, essayons d’implémenter quelques fonctions récursives. D’abord, nous allons implémenter replicate. replicate prend un Int et un élément, et retourne une liste qui a plusieurs fois cet élément. Par exemple, replicate 3 5 retourne [5, 5, 5]. Réfléchissons au cas de base. À mon avis, le cas de base correspond à des valeurs inférieures ou égales à 0. Si l’on essaie de répliquer quelque chose zéro fois, on devrai renvoyer une liste vide. Et pareil pour des nombres négatifs, sinon ça ne veut pas dire grand chose.

replicate' :: (Num i, Ord i) => i -> a -> [a]
replicate' n x
    | n <= 0    = []
    | otherwise = x:replicate' (n-1) x

Nous avons utilisé des gardes ici plutôt que des motifs car on teste une condition booléenne. Si n est plus petit que 0, retourner la liste vide. Sinon, retourner une liste qui a x comme premier élément, et ensuite x répliqué n-1 fois pour la queue. À force, la partie en (n-1) va amener notre fonction à atteindre son cas de base.

Maintenant, implémentons take. Elle prend un certain nombre d’éléments d’une liste. Par exemple, take 3 [5, 4, 3, 2, 1] retourne [5, 4, 3]. Si on essaie de prendre 0 ou moins éléments d’une liste, on récupère une liste vide. Également, si l’ont essaie de prendre quoi que ce soit d’une liste vide, on récupère une liste vide. Remarquez que ce sont nos deux cas de base. Écrivons tout cela :

take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0   = []
take' _ []     = []
take' n (x:xs) = x : take' (n-1) xs

Le premier motif spécifie qu’essayer de prendre 0 ou moins éléments retourne une liste vide. Remarquez qu’on utilise _ pour filtrer la liste parce que nous ne nous intéressons pas vraiment à sa valeur dans ce cas. Remarquez aussi qu’on utilise des gardes, mais pas otherwise. Cela veut dire que si n s’avère être supérieur à 0, le filtrage passe au motif suivant. Le deuxième motif indique que si l’on essaie de prendre quoi que ce soit dans une liste vide, on récupère une liste vide. Le troisième motif coupe la liste en tête et queue. Puis, on dit que prendre n éléments d’une liste équivaut à une liste avec x en tête et une liste qui prend n-1 éléments dans le reste pour queue. Essayez de prendre une feuille de papier pour écrire les étapes de l’évaluation de take 3 [4, 3, 2, 1].

reverse renverse une liste. Pensez au cas de base. Quel est-il ? Allons… c’est la liste vide ! Une liste vide renversée est la liste vide elle-même. Ok. Et le reste ? Eh bien, on peut dire que si l’on coupe une liste en tête et queue, la liste renversée est égale à la queue renversée, avec la tête à la fin.

reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]

Et voilà !

Puisqu’Haskell supporte des listes infinies, notre récursivité n’a pas vraiment besoin de cas de base. Si elle n’en a pas, elle va soit continuer à s’agiter sur un calcul à l’infini, ou produire une structure de donnée infinie, comme une liste infinie. La chose bien à propos des listes infinies, c’est qu’on peut les couper où on veut. repeat prend un élément et retourne une liste infinie qui a cet élément uniquement. Une implémentation récursive est très simple, regardez.

repeat' :: a -> [a]
repeat' x = x:repeat' x

Appeler repeat 3 nous donnera une liste qui commence avec un 3, et a une infinité de 3 en queue. Appeler repeat 3 s’évaluera à 3:repeat 3, puis à 3:(3:repeat 3), puis à 3:(3:(3:repeat 3)), etc. repeat 3 ne terminera jamais son évaluation, alors que take 5 (repeat 3) nous donnera une liste de cinq 3. C’est comme si on avait fait replicate 5 3.

zip prend deux listes, et les zippe ensemble. zip [1, 2, 3] [2, 3] retourne [(1, 2), (2, 3)], parce qu’elle tronque la plus grande liste pour avoir la même taille que l’autre. Et si l’on zippe quelque chose à la liste vide ? Eh bien, on obtient la liste vide. Voilà notre cas de base. Cependant, zip prend deux listes en paramètres, donc il y a en fait deux cas de base.

zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

D’abord, les deux premiers motifs disent que si une des deux listes est vide, on obtient une liste vide. Le troisième dit que deux listes zippées sont égales à la paire de leur tête, suivie de leurs queues zippées. Zipper [1, 2, 3] et ['a', 'b'] va finalement essayer de zipper [3] et []. Le cas de base arrive et le résultat est donc (1, 'a'):(2, 'b'):[], qui est exactement la même chose que [(1, 'a'), (2, 'b')].

Implémentons encore une fonction de la bibliothèque standard - elem. Elle prend un élément et une liste et vérifie si cet élément appartient à la liste. La condition de base, comme souvent, est la liste vide. On sait qu’une liste vide ne contient aucun élément, donc elle ne contient certainement pas les droïdes que vous recherchez.

elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

Plutôt simple et attendu. Si la tête n’est pas l’élément recherché, on cherche dans la queue. Si on arrive à une liste vide, le résultat est False.

Vite, triez !

Soit une liste d’éléments qui peuvent être triés. Leur type est une instance de la classe Ord. À présent, on souhaite les trier ! Il existe un algorithme très cool pour faire ça, appelé quicksort. C’est une façon très astucieuse de trier des éléments. Alors qu’elle prend facilement 10 lignes à implémenter dans des langages impératifs, l’implémentation Haskell est bien plus courte et élégante. Quicksort est devenu une sorte d’icône d’Haskell. Ainsi, implémentons le, bien qu’implémenter quicksort en Haskell est assez ringard vu que tout le monde le fait déjà pour montrer comme Haskell est élégant.

Donc, la signature de type sera quicksort :: (Ord a) => [a] -> [a]. Pas de surprise ici. Le cas de base ? La liste vide, bien sûr. Une liste vide triée est une liste vide. Maintenant, voilà l’algorithme : **une liste triée est une liste pour laquelle on a pris tous les éléments plus petits que la tête, qu’on les a triés, et placés à l’avant, puis on a mis la tête, et à la suite on a placé tous les éléments plus grands que la tête, après les avoir aussi triés“**. Remarquez comme on a dit deux fois trier dans la définition, donc il y aura probablement deux appels récursifs ! Remarquez aussi qu’on a utilisé le verbe être pour définir l’algorithme, et pas une suite de faire ceci, puis faire cela, ensuite faire ceci… C’est la beauté de la programmation fonctionnelle ! Comment allons nous filtrer d’une liste les éléments plus petits que sa tête, et ceux plus grands ? Avec des listes en compréhension. Bon, plongeons.

quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
    let smallerSorted = quicksort [a | a <- xs, a <= x]
        biggerSorted = quicksort [a | a <- xs, a > x]
    in  smallerSorted ++ [x] ++ biggerSorted

Lançons-là pour voir si elle a l’air de marcher.

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]
[1,2,2,3,3,4,4,5,6,7,8,9,10]
ghci> quicksort "the quick brown fox jumps over the lazy dog"
"        abcdeeefghhijklmnoooopqrrsttuuvwxyz"

Booyah ! Voilà de quoi je parle ! Si on a, disons [5, 1, 9, 4, 6, 7, 3] et qu’on veut la trier, cet algorithme va d’abord prendre sa tête, ici 5, et la mettre au milieu de deux listes respectivement plus petite et plus grande que la tête. À un moment, on a donc [1, 4, 3] ++ [5] ++ [9, 6, 7]. On sait qu’une fois la liste complètement triée, le 5 n’aura pas changé de place, car les 3 nombres à sa gauche sont plus petits que lui, et les 3 à sa droite sont plus grands. Maintenant, si l’on trie récursivement [1, 4, 3] et [9, 6, 7], la liste entière est triée ! On les trie à l’aide de la même fonction. Finalement, on va tellement réduire les listes qu’il ne restera que des listes vides, qui sont triées par définition, puisqu’elles sont vides. Voilà une illustration :

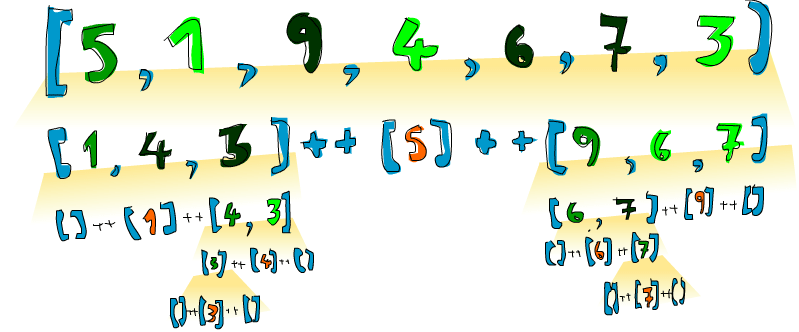
Un élément en place et qui ne bougera plus est représenté en orange. Si vous les lisez de gauche à droite, vous verrez la liste triée. Bien qu’on ait choisi de comparer tous les éléments aux têtes des listes, on aurait tout à fait pu prendre n’importe quel élément et le comparer à tous les autres. Dans quicksort, l’élément choisi pour être comparé aux autres est appelé le pivot. Ici, les pivots sont représentés en vert. Nous avons choisi la tête car il est facile de l’obtenir par filtrage par motif. Les éléments plus petits que le pivot sont en vert clair et ceux plus grands que le pivot en vert foncé. Le gradient jaune-orangé représente l’application de quicksort.

Penser récursif

Nous avons fait pas mal de récursivité et, comme vous l’avez probablement remarqué, il y a un motif sous-jacent. Généralement, vous définissez des cas de base, et ensuite une fonction qui fait quelque chose avec certains éléments et rappelle cette fonction sur le reste. Peu importe que ce soit une liste, un arbre ou une autre structure de données. Une somme est le premier élément, plus la somme du reste de la liste. Un produit est le premier élément, multiplié par le produit du reste de la liste. La longueur est 1, plus la longueur du reste de la liste. Et cætera, et cætera…

Bien sûr, il y a aussi les cas de base. Généralement, le cas de base est un scénario pour lequel un appel récursif n’a plus de sens. Pour des listes, le plus souvent c’est la liste vide. Si vous traitez des arbres, ce sera généralement une feuille, i.e. un nœud qui n’a pas d’enfants.

C’est la même chose pour traiter des nombres récursivement. Généralement, on a un nombre et une fonction appliquée à une modification de ce nombre. La factorielle vue plus tôt était le produit d’un nombre et de la factorielle de ce nombre moins un. Une telle application récursive n’a pas de sens pour zéro, parce que les factorielles sont seulement définies pour les entiers positifs. Souvent, le cas de base s’avère être un élément neutre. L’élément neutre de la multiplication est 1 car si l’on multiplie un nombre par 1, on récupère le même nombre. Lorsqu’on somme des listes, on définit la somme de la liste vide comme 0 et 0 est l’élément neutre pour l’addition. Dans quicksort, le cas de base est la liste vide et l’élément neutre est la liste vide également, car si vous rajoutez une liste vide à une autre liste, vous récupérez cette dernière.

Donc, lorsque vous essayez de penser à une solution récursive pour un problème à résoudre, essayez de vous demander quand est-ce qu’une solution récursive ne conviendra pas et d’utiliser cela comme cas de base. Pensez aux éléments neutres et demandez-vous si vous aurez à déconstruire les paramètres de la fonction (par exemple, les listes sont généralement séparées en tête et queue par un filtrage par motif) et sur quelle partie vous effectuerez un appel récursif.