Dans les chapitres précédents, nous avons vu quelques types et classes de types qui existent en Haskell. Dans ce chapitre, nous verrons comment créer les nôtres et les mettre en pratique !

Introduction aux types de données algébriques

Jusqu’ici, nous avons croisé beaucoup de types de données. Bool, Int, Char, Maybe, etc. Mais comment créer les nôtres ? Eh bien, un des moyens consiste à utiliser le mot-clé data pour définir un type. Voyons comment le type Bool est défini dans la bibliothèque standard.

data Bool = False | True

data signifie qu’on crée un nouveau type de données. La partie avant le = dénote le type, ici Bool. Les choses après le = sont des constructeurs de valeurs. Ils spécifient les différentes valeurs que peut prendre ce type. Le | se lit comme un ou. On peut donc lire cette déclaration : le type Bool peut avoir pour valeur True ou False. Le nom du type tout comme les noms des constructeurs de valeurs doivent commencer par une majuscule.

De manière similaire, on peut imaginer Int défini ainsi :

data Int = -2147483648 | -2147483647 | ... | -1 | 0 | 1 | 2 | ... | 2147483647

Le premier et le dernier constructeurs sont les valeurs minimales et maximales d’un Int. En vrai le type n’est pas défini ainsi, les points de suspension cachent l’omission d’un paquet énorme de nombres, donc ceci est juste à titre illustratif.

Maintenant, imaginons comment l’on représenterait une forme en Haskell. Une possibilité serait d’utiliser des tuples. Un cercle pourrait être (43.1, 55.0, 10.4) où les deux premières composantes seraient les coordonnées du centre, et la troisième le rayon. Ça a l’air raisonnable, mais ça pourrait tout aussi bien représenter un vecteur 3D ou je ne sais quoi. Une meilleure solution consiste à créer notre type pour représenter les données. Disons qu’une forme puisse être un cercle ou un rectangle. Voilà :

data Shape = Circle Float Float Float | Rectangle Float Float Float Float

Qu’est-ce que c’est que ça ? Pensez-y ainsi. Le constructeur de valeurs Circle a trois champs, qui sont tous des Float. Ainsi, lorsqu’on écrit un constructeur de valeurs, on peut optionnellement ajouter des types à la suite qui définissent les valeurs qu’il peut contenir. Ici, les deux premiers champs sont les coordonnées du centre, le troisième est son rayon. Le constructeur de valeurs Rectangle a quatre champs qui acceptent des Float. Les deux premiers sont les coordonnées du coin supérieur gauche, et les deux autres celles du coin inférieur droit.

Quand je dis champ, il s’agit en fait de paramètres. Les constructeurs de valeurs sont ainsi des fonctions qui retournent ultimement un type de données. Regardons les signatures de type de ces deux constructeurs de valeurs.

ghci> :t Circle
Circle :: Float -> Float -> Float -> Shape
ghci> :t Rectangle
Rectangle :: Float -> Float -> Float -> Float -> Shape

Cool, donc les constructeurs de valeurs sont des fonctions comme les autres. Qui l’eût cru ? Créons une fonction qui prend une forme et retourne sa surface.

surface :: Shape -> Float
surface (Circle _ _ r) = pi * r ^ 2
surface (Rectangle x1 y1 x2 y2) = (abs $ x2 - x1) * (abs $ y2 - y1)

La première chose notable, c’est la déclaration de type. Elle dit que la fonction prend un Shape et retourne un Float. On n’aurait pas pu écrire une déclaration de type Circle -> Float parce que Circle n’est pas un type, alors que Shape en est un. Tout comme on ne peut pas écrire une fonction qui a pour déclaration de type True -> Int. La prochaine chose remarquable, c’est le filtrage par motif sur les constructeurs de valeurs. Nous l’avons en fait déjà fait (tout le temps à vrai dire), lorsque l’on filtrait des valeurs contre [] ou False ou 5, seulement ces valeurs n’avaient pas de champs. On écrit seulement le constructeur, puis on lie ses champs à des noms. Puisqu’on s’intéresse au rayon, on se fiche des autres champs, qui n’indiquent que la position du cercle.

ghci> surface $ Circle 10 20 10
314.15927
ghci> surface $ Rectangle 0 0 100 100
10000.0

Yay, ça marche ! Mais si on essaie d’afficher Circle 10 20 5 dans l’invite, on obtient une erreur. C’est parce qu’Haskell ne sait pas (encore) comment afficher ce type de données sous une forme littérale. Rappelez-vous, quand on essaie d’afficher une valeur dans l’invite, Haskell exécute la fonction show sur cette valeur pour obtenir une représentation en chaîne de caractères, puis affiche celle-ci dans le terminal. Pour rendre Shape membre de la classe de types Show, on peut le modifier ainsi :

data Shape = Circle Float Float Float | Rectangle Float Float Float Float deriving (Show)

On ne s’intéressera pas trop à la dérivation pour l’instant. Disons seulement qu’en ajoutant deriving (Show) à la fin d’une déclaration data, Haskell rend magiquement ce type membre de la classe de types Show. Ainsi, on peut à présent faire :

ghci> Circle 10 20 5
Circle 10.0 20.0 5.0
ghci> Rectangle 50 230 60 90
Rectangle 50.0 230.0 60.0 90.0

Les constructeurs de valeurs sont des fonctions, on peut donc les mapper, les appliquer partiellement, etc. Si l’on veut créer une liste de cercles concentriques de différents rayons, on peut faire :

ghci> map (Circle 10 20) [4,5,6,6]
[Circle 10.0 20.0 4.0,Circle 10.0 20.0 5.0,Circle 10.0 20.0 6.0,Circle 10.0 20.0 6.0]

Notre type de données est satisfaisant, bien qu’il pourrait être amélioré. Créons un type de données intermédiaire qui définit un point dans l’espace bidimensionnel. On pourra l’utiliser pour rendre nos formes plus compréhensibles.

data Point = Point Float Float deriving (Show)
data Shape = Circle Point Float | Rectangle Point Point deriving (Show)

Remarquez qu’en définissant un point, on a utilisé le même nom pour le type de données et pour le constructeur de valeurs. Ça n’a pas de sens particulier, mais il est assez usuel de donner le même nom lorsqu’un type n’a qu’un seul constructeur de valeurs. À présent, le Circle a deux champs, un de type Point et un autre de type Float. Cela simplifie la compréhension de ce qu’ils représentent. Idem pour le rectangle. On doit maintenant ajuster surface pour refléter ces changements.

surface :: Shape -> Float
surface (Circle _ r) = pi * r ^ 2
surface (Rectangle (Point x1 y1) (Point x2 y2)) = (abs $ x2 - x1) * (abs $ y2 - y1)

On a seulement changé les motifs. Dans le motif du cercle, on ignore complètement le point. Dans celui du rectangle, on utilise des motifs imbriqués pour récupérer les champs des points. Si l’on voulait référencer le point lui-même pour une raison quelconque, on aurait pu utiliser des motifs nommés.

ghci> surface (Rectangle (Point 0 0) (Point 100 100))
10000.0
ghci> surface (Circle (Point 0 0) 24)
1809.5574

Et pourquoi pas une fonction qui bouge une forme ? Elle prend une forme, une quantité sur l’axe x et sur l’axe y, et retourne une forme aux mêmes dimensions, mais déplacée selon ces quantités.

nudge :: Shape -> Float -> Float -> Shape
nudge (Circle (Point x y) r) a b = Circle (Point (x+a) (y+b)) r
nudge (Rectangle (Point x1 y1) (Point x2 y2)) a b = Rectangle (Point (x1+a) (y1+b)) (Point (x2+a) (y2+b))

Plutôt simple. On ajoute simplement les déplacements aux coordonnées correspondantes.

ghci> nudge (Circle (Point 34 34) 10) 5 10
Circle (Point 39.0 44.0) 10.0

Si on ne veut pas manipuler directement les points, on peut créer des fonctions auxiliaires qui créent des formes d’une taille donnée à l’origine, puis les déplacer.

baseCircle :: Float -> Shape
baseCircle r = Circle (Point 0 0) r

baseRect :: Float -> Float -> Shape
baseRect width height = Rectangle (Point 0 0) (Point width height)
ghci> nudge (baseRect 40 100) 60 23
Rectangle (Point 60.0 23.0) (Point 100.0 123.0)

Vous pouvez bien sûr exporter vos types de données de vos modules. Pour ce faire, ajoutez simplement les types que vous souhaitez exporter au même endroit que les fonctions à exporter, puis ouvrez des parenthèses et spécifiez les constructeurs de valeurs que vous voulez exporter, séparés par des virgules. Si vous voulez exporter tous les constructeurs, vous pouvez écrire ...

Si on voulait exporter les fonctions et types définis ici dans un module, on pourrait commencer ainsi :

module Shapes
( Point(..)
, Shape(..)
, surface
, nudge
, baseCircle
, baseRect
) where

En faisant Shape(..), on exporte tous les constructeurs de valeurs de Shape, donc quiconque importe le module peut créer des formes à l’aide de Rectangle et Circle. C’est équivalent à Shape (Rectangle, Circle).

On pourrait aussi choisir de ne pas exporter de constructeurs de valeurs pour Shape en écrivant simplement Shape dans la déclaration d’export. Ainsi, quelqu’un qui voudrait créer une forme serait obligé de le faire en passant par les fonctions baseCircle et baseRect. Data.Map utilise cette approche. Vous ne pouvez pas créer de map en faisant Map.Map [(1,2),(3,4)] parce qu’il n’exporte pas ce constructeur de valeurs. Cependant, vous pouvez en créer à l’aide de fonctions auxiliaires comme Map.fromList. Souvenez-vous, les constructeurs de valeurs sont juste des fonctions qui prennent des champs en paramètres et retournent une valeur d’un certain type (comme Shape). Donc quand on choisit de ne pas les exporter, on empêche seulement les personnes qui importent notre module d’utiliser ces fonctions, mais si d’autres fonctions exportées retournent un type, on peut les utiliser pour créer des valeurs de ce type de données.

Ne pas exporter les constructeurs de valeurs d’un type de données le rend plus abstrait en cachant son implémentation. Également, quiconque utilise ce module ne peut pas filtrer par motif sur les constructeurs de valeurs.

Syntaxe des enregistrements

OK, on vient de nous donner la tâche de créer un type de données pour décrire une personne. Les informations à stocker pour décrire une personne sont : prénom, nom de famille, âge, poids, numéro de téléphone, et parfum de glace préféré. Je ne sais pas pour vous, mais c’est tout ce que je souhaite savoir à propos d’une personne. Allons-y !

data Person = Person String String Int Float String String deriving (Show)

Ok. Le premier champ est le prénom, le deuxième le nom, etc. Créons une personne.

ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
ghci> guy
Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"

Plutôt cool, bien qu’un peu illisible. Comment faire une fonction pour récupérer juste une information sur la personne ? Une pour son prénom, une pour son nom, etc. Nous devrions les définir ainsi :

firstName :: Person -> String
firstName (Person firstname _ _ _ _ _) = firstname

lastName :: Person -> String
lastName (Person _ lastname _ _ _ _) = lastname

age :: Person -> Int
age (Person _ _ age _ _ _) = age

height :: Person -> Float
height (Person _ _ _ height _ _) = height

phoneNumber :: Person -> String
phoneNumber (Person _ _ _ _ number _) = number

flavor :: Person -> String
flavor (Person _ _ _ _ _ flavor) = flavor

Wow ! Personnellement, je n’ai pas trop apprécié écrire ça ! En dépit d’être très encombrante et ENNUYEUSE à écrire, cette méthode fonctionne.

ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
ghci> firstName guy
"Buddy"
ghci> height guy
184.2
ghci> flavor guy
"Chocolate"

Il doit y avoir un meilleur moyen, vous vous dites ! Eh bien non, il n’y en a pas, désolé.

Non, je blague, il y en a un. Hahaha ! Les créateurs d’Haskell étaient très intelligents et ont anticipé ce scénario. Ils ont inclus une version alternative de l’écriture des types de données. Voici comment l’on pourrait obtenir les mêmes fonctionnalités avec une syntaxe d’enregistrements.

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     , height :: Float
                     , phoneNumber :: String
                     , flavor :: String
                     } deriving (Show)

Donc, plutôt que de seulement nommer les types des champs les uns après les autres et de les séparer par des espaces, on peut utiliser des accolades. On écrit d’abord le nom du champ, par exemple firstName, puis un :: (aussi appelé Paamayim Nekudotayim, haha) puis on spécifie son type. Le type de données résultant est exactement le même. Le principal avantage est que cela crée les fonctions pour examiner chaque champ du type de données. En utilisant la syntaxe des enregistrements, Haskell a automatiquement créé ces fonctions : firstName, lastName, age, height, phoneNumber et flavor.

ghci> :t flavor
flavor :: Person -> String
ghci> :t firstName
firstName :: Person -> String

Il y a également un autre avantage à utiliser la syntaxe des enregistrements. Lorsqu’on dérive Show pour le type, il est affiché différemment lorsqu’on utilise la syntaxe des enregistrements pour définir et instancier le type. Mettons qu’on a un type qui représente des voitures. On souhaite garder une trace de la compagnie qui l’a créée, le nom du modèle et l’année de production. Regardez.

data Car = Car String String Int deriving (Show)

ghci> Car "Ford" "Mustang" 1967
Car "Ford" "Mustang" 1967

Si on le définit à l’aide de la syntaxe des enregistrements, on peut créer une nouvelle voiture comme suit.

data Car = Car {company :: String, model :: String, year :: Int} deriving (Show)

ghci> Car {company="Ford", model="Mustang", year=1967}
Car {company = "Ford", model = "Mustang", year = 1967}

À la création de la voiture, on n’a pas nécessairement à mettre les champs dans le bon ordre, du moment qu’on les liste tous. Alors que sans la syntaxe des enregistrements, l’ordre importe.

Utilisez cette syntaxe lorsqu’un constructeur a plusieurs champs et qu’il n’est pas évident de prédire lequel correspond à quoi. Si l’on crée un type de données vecteur 3D en faisant data Vector = Vector Int Int Int, il est plutôt évident que les champs sont les trois composantes du vecteur. Par contre, pour Person ou Car, c’était plus compliqué et on a gagné à utiliser la syntaxe des enregistrements.

Paramètres de types

Un constructeur de valeurs peut prendre plusieurs valeurs comme paramètres et retourner une nouvelle valeur. Par exemple, le constructeur Car prend trois valeurs et produit une valeur de type Car. De manière similaire, les constructeurs de types peuvent prendre des types en paramètres pour créer de nouveaux types. Ça peut sembler un peu trop méta au premier abord, mais ce n’est pas si compliqué. Si vous êtes familier avec les templates C++, vous verrez des parallèles. Pour se faire une bonne image de l’utilisation des paramètres de types en action, regardons comment un des types que nous avons déjà rencontré est implémenté.

data Maybe a = Nothing | Just a

Le a est un paramètre de type. Et puisqu’il y a un paramètre de type impliqué, on dit que Maybe est un constructeur de type. En fonction de ce que l’on veut que ce type de données contienne lorsqu’il ne vaut pas Nothing, ce constructeur de types peut éventuellement construire un type Maybe Int, Maybe Car, Maybe String, etc. Aucune valeur ne peut avoir pour type Maybe, car ce n’est pas un type per se, mais un constructeur de types. Pour pouvoir être un type réel qui peut avoir une valeur, il doit avoir tous ses paramètres remplis.

Donc, si l’on passe Char en paramètre de type à Maybe, on obtient un type Maybe Char. La valeur Just 'a' a pour type Maybe Char par exemple.

Vous ne le savez peut-être pas, mais on a utilisé un type qui a un paramètre de type avant même d’utiliser Maybe. Ce type est le type des listes. Bien qu’il y ait un peu de sucre syntaxique en jeu, le type liste prend un paramètre et produit un type concret. Des valeurs peuvent avoir pour type [Int], [Char], [[String]], mais aucune valeur ne peut avoir pour type [].

Jouons un peu avec le type Maybe.

ghci> Just "Haha"
Just "Haha"
ghci> Just 84
Just 84
ghci> :t Just "Haha"
Just "Haha" :: Maybe [Char]
ghci> :t Just 84
Just 84 :: (Num t) => Maybe t
ghci> :t Nothing
Nothing :: Maybe a
ghci> Just 10 :: Maybe Double
Just 10.0

Les paramètres de types sont utiles parce qu’on peut créer différents types en fonction de la sorte de types qu’on souhaite que notre type de données contienne. Quand on fait :t Just "Haha", le moteur d’inférence de types se rend compte que le type doit être Maybe [Char], parce que le a dans le Just a est une chaîne de caractères, donc le a de Maybe a doit aussi être une chaîne de caractères.

Remarquez que le type de Nothing est Maybe a. Son type est polymorphique. Si une fonction nécessite un Maybe Int en paramètre, on peut lui donner Nothing, parce que Nothing ne contient pas de valeur de toute façon, donc peu importe. Le type Maybe a peut se comporter comme Maybe Int s’il le faut, tout comme 5 peut se comporter comme un Int ou un Double. De façon similaire, le type de la liste vide est [a]. Une liste vide peut être une liste de quoi que ce soit. C’est pourquoi on peut faire [1, 2, 3] ++ [] et ["ha", "ha", "ha"] ++ [].

Utiliser les paramètres de types est très bénéfique, mais seulement quand les utiliser a un sens. Généralement, on les utilise quand notre type de données fonctionne sans se soucier du type de ce qu’il contient en lui, comme pour notre type Maybe a. Si notre type se comporte comme une sorte de boîte, il est bien de les utiliser. On pourrait changer notre type de données Car de ceci :

data Car = Car { company :: String
               , model :: String
               , year :: Int
               } deriving (Show)

en cela :

data Car a b c = Car { company :: a
                     , model :: b
                     , year :: c
                     } deriving (Show)

Mais y gagnerait-on vraiment ? La réponse est : probablement pas, parce qu’on finirait par définir des fonctions qui ne fonctionnent que sur le type Car String String Int. Par exemple, vu notre première définition de Car, on pourrait écrire une fonction qui affiche les propriétés de la voiture avec un joli petit texte.

tellCar :: Car -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y

ghci> let stang = Car {company="Ford", model="Mustang", year=1967}
ghci> tellCar stang
"This Ford Mustang was made in 1967"

Quelle jolie petite fonction ! La déclaration de type est mignonne et fonctionne bien. Maintenant, si Car était Car a b c ?

tellCar :: (Show a) => Car String String a -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y

Nous devrions forcer cette fonction à prendre un type Car tel que (Show a) => Car String String a. Vous pouvez constater que la signature de type est plus compliquée, et le seul avantage qu’on en tire serait qu’on pourrait utiliser n’importe quel type instance de la classe de types Show pour c.

ghci> tellCar (Car "Ford" "Mustang" 1967)
"This Ford Mustang was made in 1967"
ghci> tellCar (Car "Ford" "Mustang" "nineteen sixty seven")
"This Ford Mustang was made in \"nineteen sixty seven\""
ghci> :t Car "Ford" "Mustang" 1967
Car "Ford" "Mustang" 1967 :: (Num t) => Car [Char] [Char] t
ghci> :t Car "Ford" "Mustang" "nineteen sixty seven"
Car "Ford" "Mustang" "nineteen sixty seven" :: Car [Char] [Char] [Char]

Dans la vie réelle cependant, on finirait par utiliser Car String String Int la plupart du temps, et il semblerait que paramétrer le type Car ne vaudrait pas le coup. On utilise généralement les paramètres de types lorsque le type contenu dans les divers constructeurs de valeurs du type de données n’est pas vraiment important pour que le type fonctionne. Une liste de choses est une liste de choses, peu importe ce que les choses sont, ça marche. Si on souhaite sommer une liste de nombres, on peut spécifier au dernier moment que la fonction de sommage attend une liste de nombres. De même pour Maybe. Maybe représente une option qui est soit de n’avoir rien, soit d’avoir quelque chose. Peu importe ce que le type de cette chose est.

Un autre exemple de type paramétré que nous avons déjà rencontré est Map k v de Data.Map. Le k est le type des clés, le v le type des valeurs. C’est un bon exemple d’endroit où les types paramétrés sont très utiles. Avoir des maps paramétrées nous permet de créer des maps de n’importe quel type vers n’importe quel autre type, du moment que le type de la clé soit membre de la classe de types Ord. Si nous souhaitions définir un type de map, on pourrait ajouter la contrainte de classe dans la déclaration data :

data (Ord k) => Map k v = ...

Cependant, il existe une très forte convention en Haskell qui est de ne jamais ajouter de contraintes de classe à une déclaration de données. Pourquoi ? Eh bien, parce que le bénéfice est minimal, mais on se retrouve à écrire plus de contraintes de classes, même lorsqu’elles ne sont pas nécessaires. Que l’on mette ou non, la contrainte Ord k dans la déclaration data de Map k v, on aura à écrire la contrainte dans les fonctions qui supposent un ordre sur les clés de toute façon. Mais, si l’on ne met pas la contrainte dans la déclaration data, alors on n’aura pas à mettre (Ord k) => dans les déclarations de types des fonctions qui n’ont pas besoin de cette contrainte pour fonctionner. Un exemple d’une telle fonction est toList, qui prend un mapping et le convertit en liste associative. Sa signature de type est toList :: Map k a -> [(k, a)]. Si Map k v avait une contrainte de classe dans sa déclaration data, le type de ToList devrait être toList :: (Ord k) => Map k a -> [(k, a)], alors que cette fonction ne fait aucune comparaison de clés selon leur ordre.

Conclusion : ne mettez pas de contraintes de classe dans les déclarations data même lorsqu’elles ont l’air sensées, parce que de toute manière, vous devrez les écrire dans les fonctions qui en dépendent.

Implémentons un type de vecteur 3D et ajoutons-y quelques opérations. Nous utiliserons un type paramétré afin qu’il supporte plusieurs types numériques, bien qu’en général on n’en utilise qu’un seul.

data Vector a = Vector a a a deriving (Show)

vplus :: (Num t) => Vector t -> Vector t -> Vector t
(Vector i j k) `vplus` (Vector l m n) = Vector (i+l) (j+m) (k+n)

vectMult :: (Num t) => Vector t -> t -> Vector t
(Vector i j k) `vectMult` m = Vector (i*m) (j*m) (k*m)

scalarMult :: (Num t) => Vector t -> Vector t -> t
(Vector i j k) `scalarMult` (Vector l m n) = i*l + j*m + k*n

vplus somme deux vecteurs. Deux vecteurs sont sommés en sommant leurs composantes deux à deux. scalarMult est le produit scalaire de deux vecteurs et vectMult permet de multiplier un vecteur par un scalaire. Ces fonctions peuvent opérer sur des types comme Vector Int, Vector Integer, Vector Float, à condition que le a de Vector a soit de la classe Num. Également, si vous examinez les déclarations de type des fonctions, vous verrez qu’elles n’opèrent que sur des vecteurs de même type et que les scalaires doivent également être du type contenu dans les vecteurs. Remarquez qu’on n’a pas mis de contrainte Num dans la déclaration data, puisqu’on a eu à l’écrire dans chaque fonction qui en dépendait de toute façon.

Une fois de plus, il est très important de distinguer le constructeur de types du constructeur de valeurs. Lorsqu’on déclare un type, le nom à gauche du = est le constructeur de types, et les constructeurs situés après (séparés par des |) sont des constructeurs de valeurs. Donner à une fonction le type Vector t t t -> Vector t t t -> t serait faux, parce que l’on doit donner des types dans les déclarations de types, le constructeur de types vecteurs ne prend qu’un paramètre, alors que le constructeur de valeurs en prend trois. Jouons avec nos vecteurs.

ghci> Vector 3 5 8 `vplus` Vector 9 2 8
Vector 12 7 16
ghci> Vector 3 5 8 `vplus` Vector 9 2 8 `vplus` Vector 0 2 3
Vector 12 9 19
ghci> Vector 3 9 7 `vectMult` 10
Vector 30 90 70
ghci> Vector 4 9 5 `scalarMult` Vector 9.0 2.0 4.0
74.0
ghci> Vector 2 9 3 `vectMult` (Vector 4 9 5 `scalarMult` Vector 9 2 4)
Vector 148 666 222

Instances dérivées

Dans la section Classes de types 101, nous avons vu les bases des classes de types. Nous avons dit qu’une classe de types est une sorte d’interface qui définit un comportement. Un type peut devenir une instance d’une classe de types s’il supporte ce comportement. Par exemple : le type Int est une instance d’Eq parce que cette classe définit le comportement de ce qui peut être testé pour l’égalité. Et puisqu’on peut tester l’égalité de deux entiers, Int est membre de la classe Eq. La vraie utilité vient des fonctions qui agissent comme l’interface d’Eq, à savoir == et /=. Si un type est membre d’Eq, on peut utiliser les fonctions == et /= avec des valeurs de ce type. C’est pourquoi des expressions comme 4 == 4 et "foo" /= "bar" sont correctement typées.

Nous avons aussi mentionné qu’elles sont souvent confondues avec les classes de langages comme Java, Python, C++ et autres, ce qui sème la confusion dans l’esprit de beaucoup de gens. Dans ces langages, les classes sont des patrons à partir desquels sont créés des objets qui contiennent un état et peuvent effectuer des actions. Les classes de types sont plutôt comme des interfaces. On ne crée pas de données à partir de classes de types. Plutôt, on crée d’abord notre type de données, puis on se demande pour quoi il peut se faire passer. S’il peut être comparé pour l’égalité, on le rend instance de la classe Eq. S’il peut être ordonné, on le rend instance de la classe Ord.

Dans la prochaine section, nous verrons comment créer manuellement nos instances d’une classe de types en implémentant les fonctions définies par cette classe. Pour l’instant, voyons comment Haskell peut magiquement faire de nos types des instances de n’importe laquelle des classes de types suivantes : Eq, Ord, Enum, Bounded, Show et Read. Haskell peut dériver le comportement de nos types dans ces contextes si l’on utilise le mot-clé deriving lors de la création du type de données.

Considérez ce type de données :

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     }

Il décrit une personne. Posons comme hypothèse que deux personnes n’ont jamais les mêmes nom, prénom et âge. Maintenant, si l’on a un enregistrement pour deux personnes, est-ce que cela a un sens de vérifier s’il s’agit de la même personne ? Bien sûr. On peut essayer de voir si les enregistrements sont les mêmes ou non. C’est pourquoi il serait sensé que ce type soit membre de la classe Eq. Nous allons dériver cette instance.

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     } deriving (Eq)

Lorsqu’on dérive l’instance Eq pour un type, puis qu’on essaie de comparer deux valeurs de ce type avec == ou /=, Haskell va regarder si les deux constructeurs sont égaux (ici il n’y en a qu’un possible cependant), puis va tester si les données contenues dans les valeurs sont égales deux à deux en testant chaque paire de champ avec ==. Ainsi, il y a un détail important, qui est que les types des champs doivent aussi êtres membres de la classe Eq. Puisque String et Int le sont, tout va bien. Testons notre instance d’Eq.

ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> let adRock = Person {firstName = "Adam", lastName = "Horovitz", age = 41}
ghci> let mca = Person {firstName = "Adam", lastName = "Yauch", age = 44}
ghci> mca == adRock
False
ghci> mikeD == adRock
False
ghci> mikeD == mikeD
True
ghci> mikeD == Person {firstName = "Michael", lastName = "Diamond", age = 43}
True

Bien sûr, puisque Person est maintenant dans Eq, on peut utiliser comme a pour toute fonction ayant une contrainte de classe Eq a dans sa signature, comme elem.

ghci> let beastieBoys = [mca, adRock, mikeD]
ghci> mikeD `elem` beastieBoys
True

Les classes de types Show et Read sont pour les choses qui peuvent être converties respectivement vers et depuis une chaîne de caractères. Comme avec Eq, si un constructeur de types a des champs, leur type doit aussi être membre de Show ou Read si on veut faire de notre type une instance de l’une de ces classes. Faisons de notre type de données Person un membre de Show et de Read.

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     } deriving (Eq, Show, Read)

Maintenant, on peut afficher une personne dans le terminal.

ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> mikeD
Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> "mikeD is: " ++ show mikeD
"mikeD is: Person {firstName = \"Michael\", lastName = \"Diamond\", age = 43}"

Si nous avions voulu afficher une personne dans le terminal avant de rendre Person membre de Show, Haskell se serait plaint du fait qu’il ne sache pas représenter une personne comme une chaîne de caractères. Mais maintenant qu’on a dérivé Show, il sait comment faire.

Read est en gros l’inverse de Show. Show convertit des valeurs de notre type en des chaînes de caractères, Read convertit des chaîne de caractères en valeurs de notre type. Souvenez-vous cependant, lorsqu’on avait utilisé la fonction read, on avait dû annoter explicitement le type qu’on désirait. Sans cela, Haskell ne sait pas vers quel type on veut convertir.

ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" :: Person
Person {firstName = "Michael", lastName = "Diamond", age = 43}

Si on utilise le résultat de read dans un calcul plus élaboré, Haskell peut inférer le type qu’on attend, et l’on n’a alors pas besoin d’annoter le type.

ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" == mikeD
True

On peut aussi lire des types paramétrés, et il faut alors annoter le type avec les paramètres complétés. Ainsi, on ne peut pas faire read "Just 't'" :: Maybe a, mais on peut faire read "Just 't'" :: Maybe Char.

On peut dériver des instances la classe de types Ord, qui est pour les types dont les valeurs peuvent être ordonnées. Si l’on compare deux valeurs du même type ayant été construites par deux constructeurs différents, la valeur construite par le constructeur défini en premier sera considérée plus petite. Par exemple, considérez le type Bool, qui peut avoir pour valeur False ou True. Pour comprendre comment il fonctionne lorsqu’il est comparé, on peut l’imaginer défini comme :

data Bool = False | True deriving (Ord)

Puisque le constructeur de valeurs False est spécifié avant le constructeur de valeurs True, on peut considérer que True est plus grand que False.

ghci> True `compare` False
GT
ghci> True > False
True
ghci> True < False
False

Dans le type de données Maybe a, le constructeur de valeurs Nothing est spécifié avant le constructeur de valeurs Just, donc une valeur Nothing est toujours plus petite qu’une valeur Just something, même si ce something est moins un milliard de milliards. Mais si l’on compare deux valeurs Just, alors Haskell compare ce qu’elles contiennent.

ghci> Nothing < Just 100
True
ghci> Nothing > Just (-49999)
False
ghci> Just 3 `compare` Just 2
GT
ghci> Just 100 > Just 50
True

Mais on ne peut pas faire Just (*3) > Just (*2), parce que (*3) et (*2) sont des fonctions, qui ne sont pas des instances d’Ord.

On peut facilement utiliser des types de données algébriques pour créer des énumérations, et les classes de types Enum et Bounded nous aident dans la tâche. Considérez les types de données suivants :

data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday

Puisque tous les constructeurs de valeurs sont nullaires (ils ne prennent pas de paramètres, ou champs), on peut rendre le type membre de la classe Enum. La classe de types Enum est pour les choses qui ont des prédécesseurs et des successeurs. On peut aussi le rendre membre de la classe Bounded, qui est pour les choses avec une plus petite valeur et une plus grande valeur. Tant qu’on y est, faisons-en aussi une instance des autres classes qu’on a vues.

data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday
           deriving (Eq, Ord, Show, Read, Bounded, Enum)

Puisque le type est membre des classes Show et Read, on peut le convertir vers et depuis des chaînes de caractères.

ghci> Wednesday
Wednesday
ghci> show Wednesday
"Wednesday"
ghci> read "Saturday" :: Day
Saturday

Puisqu’il est membre des classes Eq et Ord, on peut comparer et tester l’égalité de deux jours.

ghci> Saturday == Sunday
False
ghci> Saturday == Saturday
True
ghci> Saturday > Friday
True
ghci> Monday `compare` Wednesday
LT

Il est aussi membre de Bounded, donc on peut demander le plus petit jour et le plus grand jour.

ghci> minBound :: Day
Monday
ghci> maxBound :: Day
Sunday

C’est aussi une instance d’Enum. On peut obtenir le prédécesseur et le successeur d’un jour, et créer une progression de jours !

ghci> succ Monday
Tuesday
ghci> pred Saturday
Friday
ghci> [Thursday .. Sunday]
[Thursday,Friday,Saturday,Sunday]
ghci> [minBound .. maxBound] :: [Day]
[Monday,Tuesday,Wednesday,Thursday,Friday,Saturday,Sunday]

C’est plutôt génial.

Synonymes de types

Précédemment, on a mentionné qu’en écrivant des types, les types [Char] et String étaient équivalents et interchangeables. Ceci est implémenté à l’aide des synonymes de types. Les synonymes de types ne font rien per se, il s’agit simplement de donner des noms différents au même type afin que la lecture du code ou de la documentation ait plus de sens pour le lecteur. Voici comment la bibliothèque standard définit String comme un synonyme de [Char].

type String = [Char]

On a introduit le mot-clé type. Le mot-clé peut être déroutant pour certains, puisqu’on ne crée en fait rien de nouveau (on faisait cela avec le mot-clé data), mais on crée seulement un synonyme pour un type déjà existant.

Si l’on crée une fonction qui convertit une chaîne de caractères en majuscules et qu’on l’appelle toUpperString, on peut lui donner comme déclaration de type toUpperString :: [Char] -> [Char] ou toUpperString :: String -> String. Ces deux déclarations sont en effet identiques, mais la dernière est plus agréable à lire.

Quand on utilisait le module Data.Map, on a commencé par représenter un carnet téléphonique comme une liste associative avant de le représenter comme une map. Comme nous l’avions alors vu, une liste associative est une liste de paires clé-valeur. Regardons le carnet que nous avions alors.

phoneBook :: [(String,String)]
phoneBook =
    [("betty","555-2938")
    ,("bonnie","452-2928")
    ,("patsy","493-2928")
    ,("lucille","205-2928")
    ,("wendy","939-8282")
    ,("penny","853-2492")
    ]

On voit que le type de phoneBook est [(String, String)]. Cela nous indique que c’est une liste associative qui mappe des chaînes de caractères vers des chaînes de caractères, mais pas grand chose de plus. Créons un synonyme de types pour communiquer plus d’informations dans la déclaration de type.

type PhoneBook = [(String,String)]

À présent, la déclaration de notre carnet peut être phoneBook :: PhoneBook. Créons aussi un synonyme pour String.

type PhoneNumber = String
type Name = String
type PhoneBook = [(Name,PhoneNumber)]

Donner des synonymes de types au type String est pratique courante chez les programmeurs en Haskell lorsqu’ils souhaitent indiquer plus d’information à propos des chaînes de caractères qu’ils utilisent dans leur programme et ce qu’elles représentent.

À présent, lorsqu’on implémente une fonction qui prend un nom et un nombre, et cherche si cette combinaison de nom et de numéro est dans notre carnet téléphonique, on peut lui donner une description de type très jolie et descriptive.

inPhoneBook :: Name -> PhoneNumber -> PhoneBook -> Bool
inPhoneBook name pnumber pbook = (name,pnumber) `elem` pbook

Si nous n’avions pas utilisé de synonymes de types, notre fonction aurait pour type String -> String -> [(String,String)] -> Bool. Ici, la déclaration tirant parti des synonymes de types est plus facile à lire. Cependant, n’en faites pas trop. On introduit les synonymes de types pour soit décrire ce que des types existants représentent dans nos fonctions (et ainsi les déclarations de types de nos fonctions deviennent de meilleures documentations), soit lorsque quelque chose a un type assez long et répété souvent (comme [(String, String)]) et représente quelque chose de spécifique dans le contexte de nos fonctions.

Les synonymes de types peuvent aussi être paramétrés. Si on veut un type qui représente le type des listes associatives de façon assez générale pour être utilisé quelque que soit le type des clés et des valeurs, on peut faire :

type AssocList k v = [(k,v)]

Maintenant, une fonction qui récupère la valeur associée à une clé dans une liste associative peut avoir pour type (Eq k) => k -> AssocList k v -> Maybe v. AssocList est un constructeur de types qui prend deux types et produit un type concret, comme AssocList Int String par exemple.

Tout comme l’on peut appliquer partiellement des fonctions pour obtenir de nouvelles fonctions, on peut appliquer partiellement des constructeurs de types pour obtenir de nouveaux constructeurs de types. Tout comme on appelle une fonctions avec trop peu de paramètres, on peut spécifier trop peu de paramètres de types à un constructeur de types et obtenir un constructeur de types partiellement appliqué. Si l’on voulait un type qui représente une map (de Data.Map) qui va des entiers vers quelque chose, on pourrait faire soit :

type IntMap v = Map Int v

Ou bien :

type IntMap = Map Int

D’une manière ou de l’autre, le constructeur de types IntMap prend un seul paramètre qui est le type de ce vers quoi les entiers doivent pointer.

Soyez certains d’avoir bien saisi la distinction entre constructeurs de types et constructeurs de valeurs. Juste parce qu’on a créé un synonyme de types IntMap ou AssocList ne signifie pas que l’on peut faire quelque chose comme AssocList [(1, 2), (4, 5), (7, 9)]. Tout ce que cela signifie, c’est qu’on peut parler de ce type en utilisant des noms différents. On peut faire [(1, 2), (3, 5), (8, 9)] :: AssocList Int Int, ce qui va faire que les nombres à l’intérieur auront pour type Int, mais on peut continuer à utiliser cette liste comme une liste normale qui contient des paires d’entiers. Les synonymes de types (et plus généralement les types) ne peuvent être utilisés que dans la partie types d’Haskell. On se situe dans cette partie lorsqu’on définit de nouveaux types (donc, dans une déclaration data ou type), ou lorsqu’on se situe après un ::. Le :: peut être dans des déclarations de types ou pour des annotations de types.

Un autre type de données cool qui prend deux types en paramètres est Either a b. Voici grossièrement sa définition :

data Either a b = Left a | Right b deriving (Eq, Ord, Read, Show)

Il a deux constructeurs de valeurs. Si le constructeur Left est utilisé, alors le contenu a pour type a, si Right est utilisé, le contenu a pour type b. Ainsi, on peut utiliser ce type pour encapsuler une valeur qui peut avoir un type ou un autre, et lorsqu’on récupère une valeur qui a pour type Either a b, on filtre généralement par motif sur Left et Right pour obtenir différentes choses en fonction.

ghci> Right 20
Right 20
ghci> Left "w00t"
Left "w00t"
ghci> :t Right 'a'
Right 'a' :: Either a Char
ghci> :t Left True
Left True :: Either Bool b

Jusqu’ici, nous avons vu que Maybe a était principalement utilisé pour représenter des résultats de calculs qui pouvaient avoir soit échoué, soit réussi. Mais parfois, Maybe a n’est pas assez bien, parce que Nothing n’indique pas d’information autre que le fait que quelque chose a échoué. C’est bien pour les fonctions qui peuvent échouer seulement d’une façon, ou lorsqu’on se fiche de savoir comment elles ont échoué. Une recherche de clé dans Data.Map ne peut échouer que lorsqu’une clé n’était pas présente, donc on sait ce qui s’est passé. Cependant, lorsqu’on s’intéresse à comment une fonction a échoué ou pourquoi, on utilise généralement le type Either a b, où a est un type qui peut d’une certaine façon indiquer les raisons d’un éventuel échec, et b est le type du résultat d’un calcul réussi. Ainsi, les erreurs utilisent le constructeur de valeurs Left, alors que les résultats utilisent le constructeur de valeurs Right.

Exemple : un lycée a des casiers dans lesquels les étudiants peuvent ranger leurs posters de Guns’n’Roses. Chaque casier a une combinaison. Quand un étudiant veut un nouveau casier, il indique au superviseur des casiers le numéro de casier qu’il voudrait, et celui-ci lui donne le code. Cependant, si quelqu’un utilise déjà ce casier, il ne peut pas lui donner le casier, et l’étudiant doit en choisir un autre. On va utiliser une map de Data.Map pour représenter les casiers. Elle associera à chaque numéro de casier une paire indiquant si le casier est utilisé ou non, et le code du casier.

import qualified Data.Map as Map

data LockerState = Taken | Free deriving (Show, Eq)

type Code = String

type LockerMap = Map.Map Int (LockerState, Code)

Simple. On introduit un nouveau type de données pour représenter un casier occupé ou libre, et on crée un synonyme de types pour le code du casier. On crée aussi un synonyme de types pour les maps qui prennent un entier et renvoient une paire d’état et de code de casier. À présent, on va créer une fonction qui cherche le code dans une map de casiers. On va utiliser un type Either String Code pour représenter le résultat, parce que la recherche peut échouer de deux façons - le casier peut être déjà pris, auquel cas on ne peut pas dévoiler le code, ou bien le numéro de casier peut tout simplement ne pas exister. Si la recherche échoue, on va utiliser une String pour décrire ce qui s’est passé.

lockerLookup :: Int -> LockerMap -> Either String Code
lockerLookup lockerNumber map =
    case Map.lookup lockerNumber map of
        Nothing -> Left $ "Locker number " ++ show lockerNumber ++ " doesn't exist!"
        Just (state, code) -> if state /= Taken
                                then Right code
                                else Left $ "Locker " ++ show lockerNumber ++ " is already taken!"

On fait une recherche normale dans la map. Si l’on obtient Nothing, on retourne une valeur de type Left String, qui dit que le casier n’existe pas. Si on trouve le casier, on effectue une vérification supplémentaire pour voir s’il est utilisé. Si c’est le cas, on retourne Left en indiquant qu’il est déjà pris. Autrement, on retourne une valeur de type Right Code, dans laquelle on donne le code dudit casier. En fait, c’est un Right String, mais on a introduit un synonyme de types pour introduire un peu de documentation dans la déclaration de types. Voici une map à titre d’exemple :

lockers :: LockerMap
lockers = Map.fromList
    [(100,(Taken,"ZD39I"))
    ,(101,(Free,"JAH3I"))
    ,(103,(Free,"IQSA9"))
    ,(105,(Free,"QOTSA"))
    ,(109,(Taken,"893JJ"))
    ,(110,(Taken,"99292"))
    ]

Maintenant, cherchons le code de quelques casiers.

ghci> lockerLookup 101 lockers
Right "JAH3I"
ghci> lockerLookup 100 lockers
Left "Locker 100 is already taken!"
ghci> lockerLookup 102 lockers
Left "Locker number 102 doesn't exist!"
ghci> lockerLookup 110 lockers
Left "Locker 110 is already taken!"
ghci> lockerLookup 105 lockers
Right "QOTSA"

On aurait pu utiliser un Maybe a pour représenter le résultat, mais alors on ne saurait pas pour quelle raison on n’a pas pu obtenir le code. Ici, l’information en cas d’échec est dans le type de retour.

Structures de données récursives

Comme on l’a vu, un constructeur de type de données algébrique peut avoir plusieurs (ou aucun) champs et chaque champ doit avoir un type concret. Avec cela en tête, on peut créer des types dont les constructeurs ont des champs qui sont de ce même type ! Ainsi, on peut créer des types de données récursifs, où une valeur d’un type peut contenir des valeurs de ce même type, qui à leur tour peuvent contenir encore plus de valeurs de ce type, et ainsi de suite.

Pensez à cette liste : [5]. C’est juste un sucre syntaxique pour 5:[]. À gauche de :, il y a une valeur, et à droite, il y a une liste. Dans ce cas, c’est une liste vide. Maintenant, qu’en est-il de [4, 5] ? Eh bien, ça se désucre en 4:(5:[]). En considérant le premier :, on voit qu’il prend aussi un élément à gauche et une liste (ici 5:[]) à droite. Il en va de même pour 3:(4:(5:(6:[]))), qui peut aussi être écrit 3:4:5:6:[] (parce que : est associatif à droite) ou [3, 4, 5, 6].

On peut dire qu’une liste peut être la liste vide ou composée d’un élément adjoint via : à une autre liste (qui peut être vide ou non).

Utilisons un type de données algébrique pour implémenter nos propres listes dans ce cas !

data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)

On peut lire ça comme la définition des listes donnée dans un paragraphe ci-dessus. Une liste est soit vide, soit une combinaison d’une tête qui a une valeur et d’une autre liste. Si cela vous laisse perplexe, peut-être que vous serez plus à l’aise avec une syntaxe d’enregistrements.

data List a = Empty | Cons { listHead :: a, listTail :: List a} deriving (Show, Read, Eq, Ord)

Vous serez peut-être aussi surpris par le nom du constructeur Cons ici. cons est un autre nom de :. Vous voyez, pour les listes, : est en réalité un constructeur qui prend une valeur et une autre liste, pour retourner une liste. On peut d’ores et déjà utiliser notre nouveau type de listes ! Il a deux champs. Le premier de type a et le second de type List a.

ghci> Empty
Empty
ghci> 5 `Cons` Empty
Cons 5 Empty
ghci> 4 `Cons` (5 `Cons` Empty)
Cons 4 (Cons 5 Empty)
ghci> 3 `Cons` (4 `Cons` (5 `Cons` Empty))
Cons 3 (Cons 4 (Cons 5 Empty))

On a appelé notre constructeur Cons de façon infixe pour souligner sa similarité avec :. Empty est similaire à [] et 4 `Cons` (5 `Cons` Empty) est similaire à 4:(5:[]).

On peut définir des fonctions comme automatiquement infixes en ne les nommant qu’avec des caractères spéciaux. On peut aussi faire de même avec les constructeurs, puisque ce sont des fonctions qui retournent un type de données. Regardez ça !

infixr 5 :-:
data List a = Empty | a :-: (List a) deriving (Show, Read, Eq, Ord)

Tout d’abord, on remarque une nouvelle construction syntaxique, la déclaration de fixité. Lorsqu’on définit des fonctions comme opérateurs, on peut leur donner une fixité (ce n’est pas nécessaire). Une fixité indique avec quelle force un opérateur lie, et s’il est associatif à droite ou à gauche. Par exemple, la fixité de * est infixl 7 *, et la fixité de + est infixl 6. Cela signifie qu’ils sont tous deux associatifs à gauche (4 * 3 * 2 est équivalent à (4 * 3) * 2)), mais * lie plus fortement que +, car il a une plus grande fixité, et ainsi 5 * 4 + 3 est équivalent à (5 * 4) + 3.

À part ce détail, on a juste écrit a :-: (List a) à la place de Cons a (List a). Maintenant, on peut écrire des listes qui ont notre type de listes de la sorte :

ghci> 3 :-: 4 :-: 5 :-: Empty
(:-:) 3 ((:-:) 4 ((:-:) 5 Empty))
ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> 100 :-: a
(:-:) 100 ((:-:) 3 ((:-:) 4 ((:-:) 5 Empty)))

Lorsqu’on dérive Show pour notre type, Haskell va toujours afficher le constructeur comme une fonction préfixe, d’où le parenthésage autour de l’opérateur (rappelez-vous, 4 + 3 est juste (+) 4 3).

Créons une fonction qui somme deux de nos listes ensemble. ++ est défini ainsi pour des listes normales :

infixr 5  ++
(++) :: [a] -> [a] -> [a]
[]     ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)

On va juste voler cette définition pour nos listes. On nommera la fonction .++.

infixr 5  .++
(.++) :: List a -> List a -> List a
Empty .++ ys = ys
(x :-: xs) .++ ys = x :-: (xs .++ ys)

Voyons si ça a marché…

ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> let b = 6 :-: 7 :-: Empty
ghci> a .++ b
(:-:) 3 ((:-:) 4 ((:-:) 5 ((:-:) 6 ((:-:) 7 Empty))))

Bien. Très bien. Si l’on voulait, on pourrait implémenter toutes les fonctions qui opèrent sur des listes pour notre propre type liste.

Notez comme on a filtré sur le motif (x :-: xs). Cela fonctionne car le filtrage par motif n’est en fait basé que sur la correspondance des constructeurs. On peut filtrer sur :-: parce que c’est un constructeur de notre type de liste, tout comme on pouvait filtrer sur : pour des listes normales car c’était un de leurs constructeurs. Pareil pour []. Puisque le filtrage par motif marche (uniquement) sur les constructeurs, on peut filtrer sur des choses comme des constructeurs normaux préfixes, ou bien comme 8 ou 'a', qui sont simplement des constructeurs de types numériques ou de caractères respectivement.

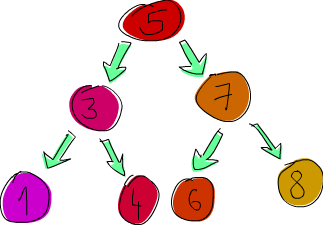
À présent, implémentons un arbre binaire de recherche. Si vous ne connaissez pas les arbres binaires de recherche, voici en quoi ils consistent : chaque élément pointe vers deux éléments, son fils gauche et son fils droit. Le fils gauche a une valeur inférieure à celle de l’élément, le fils droit a une valeur supérieure. Chacun des fils peut à son tour pointer vers zéro, un ou deux éléments. Chaque élément a ainsi au plus deux sous-arbres. Et la propriété intéressante de ces arbres est que tous les nœuds du sous-arbre gauche d’un nœud donné, mettons 5, ont une valeur inférieure à 5. Quant aux nœuds du sous-arbre droit, ils sont tous supérieurs à 5. Ainsi, si l’on cherche 8 dans un arbre dont la racine vaut 5, on va chercher seulement dans le sous-arbre droit, puisque 8 est plus grand que 5. Si le nœud suivant est 7, on cherche encore à droite car 8 est plus grand que 7. Et voilà ! On a trouvé notre élément en seulement 3 coups ! Si l’on cherchait dans une liste, ou dans un arbre mal construit, cela pourrait nous prendre jursqu’à 8 coups pour savoir si 8 est là ou pas.

Les ensembles de Data.Set et les maps de Data.Map sont implémentés à l’aide d’arbres binaires de recherche équilibrés, qui sont toujours bien équilibrés. Mais pour l’instant, nous allons simplement implémenter des arbres de recherches binaires standards.

Voilà ce qu’on va dire : un arbre est soit vide, soit un élément contenant une valeur et deux arbres. Ça sent le type de données algébrique à plein nez !

data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)

Ok, bien, c’est très bien. Plutôt que de construire des arbres à la main, on va créer une fonction qui prend un arbre, un élément, et insère cet élément. Cela se fait en comparant la valeur de l’élément que l’on souhaite insérer avec le nœud racine, s’il est plus petit on part à gauche, s’il est plus grand on part à droite. On fait de même avec tous les nœuds suivants jusqu’à ce qu’on arrive à un arbre vide. C’est ici qu’on doit insérer notre nœud qui va simplement remplacer ce vide.

Dans des langages comme C, on fait ceci en modifiant des pointeurs et des valeurs dans l’arbre. En Haskell, on ne peut pas vraiment modifier l’arbre, donc on recrée un nouveau sous-arbre chaque fois qu’on décide d’aller à gauche ou à droite et au final, la fonction d’insertion construit un tout nouvel arbre, puisqu’Haskell n’a pas de concept de pointeurs mais seulement de valeurs. Ainsi, le type de la fonction d’insertion sera de la forme a -> Tree a -> Tree a. Elle prend un élément et un arbre et retourne un nouvel arbre qui contient cet élément. Ça peut paraître inefficace, mais la paresse se charge de ce problème.

Voici donc deux fonctions. L’une est une fonction auxiliaire pour créer un arbre singleton (qui ne contient qu’un nœud) et l’autre est une fonction d’insertion.

singleton :: a -> Tree a
singleton x = Node x EmptyTree EmptyTree

treeInsert :: (Ord a) => a -> Tree a -> Tree a
treeInsert x EmptyTree = singleton x
treeInsert x (Node a left right)
    | x == a = Node x left right
    | x < a  = Node a (treeInsert x left) right
    | x > a  = Node a left (treeInsert x right)

La fonction singleton est juste un raccourci pour créer un nœud contenant une valeur et deux sous-arbres vides. Dans la fonction d’insertion, on a d’abord notre cas de base sous forme d’un motif. Si l’on atteint un arbre vide et qu’on veut y insérer notre valeur, cela veut dire qu’il faut renvoyer l’arbre singleton qui contient cette valeur. Si l’on insère dans un arbre non vide, il faut vérifier quelques choses. Si l’élément qu’on veut insérer est égal à la racine, alors on retourne le même arbre. S’il est plus petit, on retourne un arbre qui a la même racine, le même sous-arbre droit, mais qui a pour sous-arbre gauche le même qu’avant auquel on a ajouté l’élément à ajouter. Le raisonnement est symétrique si l’élément à ajouter est plus grand que l’élément à la racine.

Ensuite, on va créer une fonction qui vérifie si un élément est dans l’arbre. Définissons d’abord le cas de base. Si on cherche un élément dans l’arbre vide, il n’est certainement pas là. Ok. Voyez comme le cas de base est similaire au cas de base lorsqu’on cherche un élément dans une liste. Si on cherche un élément dans une liste vide, il n’est sûrement pas là. Enfin bon, si l’arbre n’est pas vide, quelques vérifications. Si l’élément à la racine est celui qu’on cherche, trouvé ! Sinon, eh bien ? Puisqu’on sait que les éléments à gauche sont plus petits que lui, si on cherche un élément plus petit, on va le chercher à gauche. Symétriquement, on cherchera à droite un élément plus grand que celui à la racine.

treeElem :: (Ord a) => a -> Tree a -> Bool
treeElem x EmptyTree = False
treeElem x (Node a left right)
    | x == a = True
    | x < a  = treeElem x left
    | x > a  = treeElem x right

Tout ce qu’on a eu à faire, c’est réécrire le paragraphe précédent en code. Amusons-nous avec nos arbres ! Plutôt que d’en créer un à la main (bien que ce soit possible), créons-en un à l’aide d’un pli sur une liste. Souvenez-vous, à peu près tout ce qui traverse une liste et retourne une valeur peut être implémenté comme un pli ! On va commencer avec un arbre vide, puis approcher une liste par la droite en insérant les éléments un à un dans l’arbre accumulateur.

ghci> let nums = [8,6,4,1,7,3,5]
ghci> let numsTree = foldr treeInsert EmptyTree nums
ghci> numsTree
Node 5 (Node 3 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 7 (Node 6 EmptyTree EmptyTree) (Node 8 EmptyTree EmptyTree))

Dans ce foldr, treeInsert était la fonction de pliage (elle prend un arbre, un élément d’une liste et produit un nouvel arbre) et EmptyTree était l’accumulateur initial. nums, évidemment, était la liste qu’on pliait.

Lorsqu’on affiche notre arbre à la console, il n’est pas très lisible, mais en essayant, on peut voir sa structure. On peut voir que le nœud racine est 5 et qu’il a deux sous-arbres, un qui a pour nœud racine 3, l’autre qui a pour nœud racine 7, etc.

ghci> 8 `treeElem` numsTree
True
ghci> 100 `treeElem` numsTree
False
ghci> 1 `treeElem` numsTree
True
ghci> 10 `treeElem` numsTree
False

Tester l’appartenance fonctionne aussi correctement. Cool.

Comme vous le voyez, les structures de données algébriques sont des concepts cools et puissants en Haskell. On peut les utiliser pour tout faire, des booléens et énumérations des jours de la semaine jusqu’aux arbres binaires de recherche, et encore plus !

Classes de types 102

Jusqu’ici, on a découvert des classes de types standard d’Haskell et on a vu quels types les habitaient. On a aussi appris à créer automatiquement des instances de ces classes en demandant à Haskell de les dériver pour nous. Dans cette section, on va créer nos propres classes de types, et nos propres instances, le tout à la main.

Bref récapitulatif sur les classes de types : elles sont comme des interfaces. Une classe de types définit un comportement (tester l’égalité, comparer l’ordre, énumérer), puis les types qui peuvent se comporter de la sorte sont fait instances de ces classes. Le comportement des classes de types est défini en définissant des fonctions ou juste des déclarations de types que les instances doivent implémenter. Ainsi, lorsqu’on dit qu’un type est une instance d’une classe de types, on veut dire qu’on peut utiliser les fonctions que cette classe définit sur des éléments de ce type.

Les classes de types n’ont presque rien à voir avec les classes dans des langages comme Java ou Python. Cela désoriente beaucoup de gens, aussi je veux que vous oubliiez tout ce que vous savez des classes dans les langages impératifs à partir de maintenant.

Par exemple, la classe Eq est pour les choses qui peuvent être testées égales. Elle définit les fonctions == et /=. Si on a un type (mettons, Car) et que comparer deux voitures avec == a un sens, alors il est sensé de rendre Car instance d’Eq.

Voici comment Eq est définie dans le prélude :

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool
    x == y = not (x /= y)
    x /= y = not (x == y)

Wow, wow, wow ! Quels nouveaux syntaxe et mots-clés étranges ! Pas d’inquiétude, tout cela va s’éclaircir bientôt. Tout d’abord, quand on écrit class Eq a where, cela signifie qu’on définit une nouvelle classe Eq. Le a est une variable de types et indique que a jouera le rôle du type qu’on souhaitera bientôt rendre instance d’Eq. Cette variable n’a pas à s’appeler a, ou même à être une lettre, elle doit juste être un mot en minuscules. Ensuite, on définit plusieurs fonctions. Il n’est pas obligatoire d’implémenter le corps de ces fonctions, on doit juste spécifier les déclarations de type des fonctions.

Toutefois, on a implémenté le corps des fonctions que Eq définit, mais on les a définies en termes de récursion mutuelle. On a dit que deux instances d’Eq sont égales si elles ne sont pas différentes, et différentes si elles ne sont pas égales. Ce n’était pas nécessaire, mais on l’a fait, et on va bientôt voir en quoi cela nous aide.

Maintenant qu’on a une classe, que faire avec ? Eh bien, pas grand chose, vraiment. Mais une fois qu’on a des instances, on commence à bénéficier de fonctionnalités sympathiques. Regardez donc ce type :

data TrafficLight = Red | Yellow | Green

Il définit les états d’un feu de signalisation. Voyez comme on n’a pas dérivé d’instances de classes. C’est parce qu’on va les écrire à la main, bien qu’on aurait pu dériver celles-ci pour des classes comme Eq et Show. Voici comment on fait de notre type une instance d’Eq.

instance Eq TrafficLight where
    Red == Red = True
    Green == Green = True
    Yellow == Yellow = True
    _ == _ = False

On l’a fait en utilisant le mot-clé instance. class définit de nouvelles classes de types, et instance définit de nouvelles instances d’une classe de types. Quand nous définissions Eq, on a écrit class Eq a where et on a dit que a jouait le rôle du type qu’on voudra rendre instance de la classe plus tard. On le voit clairement ici, puisque quand on crée une instance, on écrit instance Eq TrafficLight where. On a remplacé le a par le type réel de cette instance particulière.

Puisque == était défini en termes de /= et vice versa dans la déclaration de classe, il suffit d’en définir un dans l’instance pour obtenir l’autre automatiquement. On dit que c’est une définition complète minimale d’une classe de types - un des plus petits ensembles de fonctions à implémenter pour que le type puisse se comporter comme une instance de la classe. Pour remplir la définition complète minimale d’Eq, il faut redéfinir soit ==, soit /=. Cependant, si Eq était définie seulement ainsi :

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool

alors nous aurions dû implémenter ces deux fonctions lors de la création d’une instance, car Haskell ne saurait pas comment elles sont reliées. La définition complète minimale serait alors : == et /=.

Vous pouvez voir qu’on a implémenté == par un simple filtrage par motif. Puisqu’il y a beaucoup de cas où deux lumières sont différentes, on a spécifié les cas d’égalité, et utilisé un motif attrape-tout pour dire que dans tous les autres cas, les lumières sont différentes.

Créons une instance de Show à la main également. Pour satisfaire une définition complète minimale de Show, il suffit d’implémenter show, qui prend une valeur et retourne une chaîne de caractères.

instance Show TrafficLight where
    show Red = "Red light"
    show Yellow = "Yellow light"
    show Green = "Green light"

Encore une fois, nous avons utilisé le filtrage par motif pour arriver à nos fins. Voyons cela en action :

ghci> Red == Red
True
ghci> Red == Yellow
False
ghci> Red `elem` [Red, Yellow, Green]
True
ghci> [Red, Yellow, Green]
[Red light,Yellow light,Green light]

Joli. On aurait pu simplement dériver Eq et obtenir la même chose (on ne l’a pas fait, dans un but éducatif). Cependant, dériver Show aurait simplement traduit les constructeurs en chaînes de caractères. Si on veut afficher "Reg light", il faut faire la déclaration d’instance à la main.

Vous pouvez également créer des classes de types qui sont des sous-classes d’autres classes de types. La déclaration de classe de Num est un peu longue, mais elle débute ainsi :

class (Eq a) => Num a where
   ...

Comme on l’a mentionné précédemment, il y a beaucoup d’endroits où l’on peut glisser des contraintes de classe. Ici c’est comme écrire class Num a where, mais on déclare que a doit être une instance d’Eq au préalable. Ainsi, un type doit être une instance d’eq avant de pouvoir prétendre être une instance de Num. Il est logique qu’avant qu’un type soit considéré comme numérique, on puisse attendre de lui qu’il soit testable pour l’égalité. C’est tout pour le sous-typage, c’est seulement une contrainte de classes sur une déclaration de classe ! À partir de là, quand on définit le corps des fonctions, que ce soit dans la déclaration de classe ou bien dans une déclaration d’instance, on peut toujours présumer que a est membre d’Eq et ainsi utiliser == sur des valeurs de ce type.

Mais comment est-ce que Maybe, ou le type des listes, sont rendus instances de classes de types ? Ce qui rend Maybe différent de, par exemple, TrafficLight, c’est que Maybe tout seul n’est pas un type concret, mais un constructeur de types qui prend un type en paramètre (comme Char ou un autre) pour produire un type concret (comme Maybe Char). Regardons à nouveau la classe de types Eq :

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool
    x == y = not (x /= y)
    x /= y = not (x == y)

De ces déclarations de types, on voit que a est utilisé comme un type concret car tous les types entre les flèches d’une fonction doivent être concrets (souvenez-vous, on ne peut avoir de fonction de type a -> Maybe, mais on peut avoir des fonctions a -> Maybe a ou Maybe Int -> Maybe String). C’est pour cela qu’on ne peut pas faire :

instance Eq Maybe where
    ...

Parce que, comme on l’a vu, a doit être un type concret, et Maybe ne l’est pas. C’est un constructeur de types qui prend un paramètre pour produire un type concret. Il serait également très fastidieux d’écrire des instances instance Eq (Maybe Int) where, instance Eq (Maybe Char) where, etc. pour chaque type qu’on utilise. Ainsi, on peut écrire :

instance Eq (Maybe m) where
    Just x == Just y = x == y
    Nothing == Nothing = True
    _ == _ = False

C’est-à-dire qu’on déclare tous les types de la forme Maybe something comme instances d’Eq. On aurait à vrai dire pu écrire (Maybe something), mais on opte généralement pour des identifiants en une lettre pour rester proche du style Haskell. Le (Maybe m) ici joue le rôle du a de class Eq a where. Alors que Maybe n’était pas un type concret, Maybe m l’est. En spécifiant un paramètre de type (m, qui est en minuscule), on dit qu’on souhaite parler de tous les types de la forme Maybe m, où m est n’importe quel type, afin d’en faire une instance d’Eq.

Il y a un problème à cela tout de même. Le voyez-vous ? On utilise == sur le contenu de Maybe, mais on n’a pas de garantie que ce que contient Maybe est membre d’Eq ! C’est pourquoi nous devons modifier la déclaration d’instance ainsi :

instance (Eq m) => Eq (Maybe m) where
    Just x == Just y = x == y
    Nothing == Nothing = True
    _ == _ = False

On a dû ajouter une contrainte de classe ! Avec cette déclaration d’instance, on dit ceci : nous voulons que tous les types de la forme Maybe m soient membres de la classe Eq, à condition que le type m (celui dans le Maybe) soit lui-même membre d’Eq. C’est ce qu’Haskell dériverait d’ailleurs.

La plupart du temps, les contraintes de classe dans les déclarations de classes sont utilisées pour faire d’une classe de types une sous-classe d’une autre classe de types, alors que les contraintes de classe dans les déclarations d’instance sont utilisées pour exprimer des pré-requis sur le contenu de certains types. Par exemple, ici nous avons requis que le contenu de Maybe soit membre de la classe Eq.

Quand vous faites des instances, si vous voyez qu’un type est utilisé comme un type concret dans les déclarations de type de la classe (comme le a dans a -> a -> Bool), alors il faut fournir à l’instance un type concret en fournissant si besoin est des paramètres de type et en parenthésant le tout, de manière à obtenir un type concret.

Oh, encore un truc, regardez ça ! Si vous voulez connaître les instances d’une classe de types, faites juste :info YourTypeClass dans GHCi. En tapant :info Num, vous verrez toutes les fonctions que définit cette classe de types, suivies d’une liste de tous les types qui habitent cette classe. :info marche aussi sur les types et les constructeurs de types. :info Maybe vous montre toutes les classes dont Maybe est une instance. :info peut aussi montrer la déclaration de type d’une fonction. Je trouve ça plutôt cool.

Une classe de types oui-non

En JavaScript et dans d’autres langages à typage faible, on peut mettre quasiment ce que l’on veut dans une expression if. Par exemple, tout ceci est valide : if (0) alert ("YEAH") else alert("NO!"), if ("") alert ("YEAH") else alert("NO!"), if (false) alert ("YEAH") else alert("NO!"), etc. et tout cela lancera une alerte NO!. Si vous faites if ("WHAT") alert ("YEAH") else alert("NO!"), une alerte "YEAH!" sera lancée parce que JavaScript considère toutes les chaînes de caractères non vides comme des sortes de valeurs vraies.

Bien qu’utiliser Bool pour une sémantique booléenne marche mieux en Haskell, implémentons un fonctionnement à la JavaScript pour le fun ! Commençons par une déclaration de classe.

class YesNo a where
    yesno :: a -> Bool

Plutôt simple. La classe YesNo définit une seule fonction. Cette fonction prend une valeur d’un type qui peut représenter le concept de vérité, et nous indique si cette valeur est vraie ou fausse. Remarquez que la façon dont on utilise a dans cette déclaration implique que a doit être un type concret.

Ensuite, définissons des instances. Pour les nombres, on va dire que tout nombre qui n’est pas 0 est vrai, et que 0 est faux (comme en JavaScript).

instance YesNo Int where
    yesno 0 = False
    yesno _ = True

Les listes vides (et par extension les chaînes de caractères vides) sont des valeurs fausses, alors que les listes ou chaînes non vides sont des valeurs vraies.

instance YesNo [a] where
    yesno [] = False
    yesno _ = True

Remarquez qu’on a ajouté un paramètre de type a ici pour faire de la liste un type concret, bien qu’on n’ait pas ajouté de contrainte sur ce que la liste contient. Quoi d’autre, hmmm… Je sais, Bool aussi contient la notion de vérité, et c’est plutôt évident de savoir lequel est quoi.

instance YesNo Bool where
    yesno = id

Hein ? Qu’est-ce qu’id ? C’est juste une fonction de la bibliothèque standard qui prend un paramètre et retourne la même chose, ce qui correspond à ce qu’on écrirait ici de toute façon.

Faisons de Maybe a une instance.

instance YesNo (Maybe a) where
    yesno (Just _) = True
    yesno Nothing = False

Pas besoin de contrainte de classe puisqu’on ne fait aucune supposition sur ce que contient le Maybe. On a juste considéré que toute valeur Just est vraie, alors que Nothing est faux. Il a encore fallu écrire (Maybe a) plutôt que Maybe tout court, parce qu’en y réfléchissant, une fonction Maybe -> Bool ne peut pas exister (car Maybe n’est pas un type concret), alors que Maybe a -> Bool est bien et propre. Cependant, c’est plutôt cool puisqu’à présent, tout type de la forme Maybe something est membre de YesNo, peu importe ce que something est.

Précédemment, on a défini un type Tree a, qui représentait un arbre binaire de recherche. On peut dire qu’un arbre vide est faux, alors qu’un arbre non vide est vrai.

instance YesNo (Tree a) where
    yesno EmptyTree = False
    yesno _ = True

Est-ce qu’un feu tricolore peut être une valeur vraie ou fausse ? Bien sûr. Si c’est rouge, on s’arrête. Si c’est vert, on y va. Si c’est jaune ? Eh, personnellement je foncerai pour l’adrénaline.

instance YesNo TrafficLight where
    yesno Red = False
    yesno _ = True

Cool, on a plein d’instances, jouons avec !

ghci> yesno $ length []
False
ghci> yesno "haha"
True
ghci> yesno ""
False
ghci> yesno $ Just 0
True
ghci> yesno True
True
ghci> yesno EmptyTree
False
ghci> yesno []
False
ghci> yesno [0,0,0]
True
ghci> :t yesno
yesno :: (YesNo a) => a -> Bool

Bien, ça marche ! Faisons une fonction qui copie le comportement de if, mais avec des valeurs YesNo.

yesnoIf :: (YesNo y) => y -> a -> a -> a
yesnoIf yesnoVal yesResult noResult = if yesno yesnoVal then yesResult else noResult

Plutôt direct. Elle prend une valeur YesNo et deux choses. Si la valeur est plutôt vraie, elle retourne la première chose, sinon elle retourne la deuxième.

ghci> yesnoIf [] "YEAH!" "NO!"
"NO!"
ghci> yesnoIf [2,3,4] "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf True "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf (Just 500) "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf Nothing "YEAH!" "NO!"
"NO!"

La classe de types Functor

Jusqu’ici, nous avons rencontré pas mal de classes de types de la bibliothèque standard. On a joué avec Ord, pour les choses qu’on peut ranger en ordre. On s’est familiarisé avec Eq, pour les choses dont on peut tester l’égalité. On a vu Show, qui présente une interface pour les choses qui peuvent être affichées sous une forme de chaîne de caractères. Notre bon ami Read est là lorsqu’on veut convertir des chaînes de caractères en des valeurs d’un certain type. Et maintenant, on va regarder la classe de types Functor, qui est simplement pour les choses sur lesquelles on peut mapper. Vous pensez probablement aux listes à l’instant, puisque mapper sur des listes est un idiome prédominant en Haskell. Et vous avez raison, le type des listes est bien membre de la classe Functor.

Quel meilleur moyen de connaître Functor que de regarder son implémentation ? Jetons un coup d’œil.

class Functor f where
    fmap :: (a -> b) -> f a -> f b

Parfait. On voit que la classe définit une fonction, fmap, et ne fournit pas d’implémentation par défaut. Le type de fmap est intéressant. Jusqu’ici, dans les définitions de classes de types, la variable de type qui jouait le rôle du type dans la classe de type était un type concret, comme le a dans (==) :: (Eq a) => a -> a -> Bool. Mais maintenant, le f n’est pas un type concret (un type qui peut contenir des valeurs, comme Int, Bool ou Maybe String), mais un constructeur de types qui prend un paramètre de type. Petit rafraîchissement par l’exemple : Maybe Int est un type concret, mais Maybe est un constructeur qui prend un type en paramètre. Bon, on voit que fmap prend une fonction d’un type vers un autre type et un foncteur appliqué au premier type, et retourne un foncteur appliqué au second type.

Si cela semble un peu confus, ne vous inquiétez pas. Tout sera bientôt révélé avec des exemples. Hmm, cette déclaration de type de fmap me rappelle quelque chose. Si vous ne connaissez pas la signature de map, c’est map :: (a -> b) -> [a] -> [b].

Ah, intéressant ! Elle prend une fonction d’un type vers un autre type, une liste du premier type, et retourne une liste du second type. Mes amis, je crois que nous avons là un foncteur ! En fait, map est juste le fmap des listes. Voici l’instance de Functor pour les listes.

instance Functor [] where
    fmap = map

C’est tout ! Remarquez qu’on n’a pas écrit instance Functor [a] where, parce qu’en regardant fmap :: (a -> b) -> f a -> f b, on voit que f doit être un constructeur de types qui prend un type. [a] est déjà un type concret (d’une liste contenant n’importe quel type), alors que [] est un constructeur de types qui prend un type et produit des types comme [Int], [String] ou même [[String]].

Puisque pour les listes, fmap est juste map, on obtient les mêmes résultats en utilisant l’un ou l’autre sur des listes.

ghci> fmap (*2) [1..3]
[2,4,6]
ghci> map (*2) [1..3]
[2,4,6]

Que se passe-t-il lorsqu’on map ou fmap sur une liste vide ? Eh bien, bien sûr, on obtient une liste vide. On transforme simplement une liste vide de type [a] en une liste vide de type [b].

Tous les types qui peuvent se comporter comme des boîtes peuvent être des foncteurs. Vous pouvez imaginer une liste comme une boîte ayant une infinité de petits compartiments, et ils peuvent être soit tous vides, soit partiellement remplis. Donc, quoi d’autre qu’une liste peut être assimilé à une boîte ? Pour commencer, le type Maybe a. C’est comme une boîte qui peut contenir soit rien, auquel cas elle a la valeur Nothing, soit un élément, comme "HAHA", auquel cas elle a la valeur Just "HAHA". Voici comment Maybe est fait foncteur.

instance Functor Maybe where
    fmap f (Just x) = Just (f x)
    fmap f Nothing = Nothing

Encore une fois, remarquez qu’on a écrit instance Functor Maybe where et pas instance Functor (Maybe m) where, contrairement à ce qu’on avait fait avec Maybe dans YesNo. Functor veut un constructeur de types qui prend un paramètre, pas un type concret. Si vous remplacez mentalement les f par des Maybe, fmap agit comme (a -> b) -> Maybe a -> Maybe b pour ce type, ce qui semble correct. Par contre, si vous remplacez mentalement f par (Maybe m), alors elle devrait agir comme (a -> b) -> Maybe m a -> Maybe m b, ce qui n’a pas de sens puisque Maybe ne prend qu’un seul paramètre de type.

Bon, l’implémentation de fmap est plutôt simple. Si c’est une valeur vide Nothing, alors on retourne Nothing. Si on mappe sur une boîte vide, on obtient une boîte vide. C’est sensé. Tout comme mapper sur une liste vide retourne une liste vide. Si ce n’est pas une valeur vide, mais plutôt une valeur emballée dans un Just, alors on applique la fonction sur le contenu du Just.

ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") (Just "Something serious.")
Just "Something serious. HEY GUYS IM INSIDE THE JUST"
ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") Nothing
Nothing
ghci> fmap (*2) (Just 200)
Just 400
ghci> fmap (*2) Nothing
Nothing

Une autre chose sur laquelle on peut mapper, et donc en faire une instance de Functor, c’est notre type Tree a. On peut l’imaginer comme une boîte qui peut contenir zéro ou plusieurs valeurs, et le constructeur de type Tree prend exactement un paramètre de type. Si vous regardez fmap comme une fonction sur les Tree, sa signature serait (a -> b) -> Tree a -> Tree b. On va utiliser de la récursivité pour celui-là. Mapper sur un arbre vide produira un arbre vide. Mapper sur un arbre non vide donnera un arbre où notre fonction sera appliquée sur le nœud racine, et les deux sous-arbres correspondront aux sous-arbres du nœud de départ sur lesquels on aura mappé la même fonction.

instance Functor Tree where
    fmap f EmptyTree = EmptyTree
    fmap f (Node x leftsub rightsub) = Node (f x) (fmap f leftsub) (fmap f rightsub)

ghci> fmap (*2) EmptyTree
EmptyTree
ghci> fmap (*4) (foldr treeInsert EmptyTree [5,7,3,2,1,7])
Node 28 (Node 4 EmptyTree (Node 8 EmptyTree (Node 12 EmptyTree (Node 20 EmptyTree EmptyTree)))) EmptyTree

Joli ! Et pourquoi pas Either a b à présent ? Peut-on en faire un foncteur ? La classe de types Functor veut des constructeurs de types à un paramètre de type, mais Either en prend deux. Hmmm ! Je sais, on va partiellement appliquer Either en lui donnant un paramètre de type, de façon à ce qu’il n’ait plus qu’un paramètre libre. Voici comment Either a est fait foncteur dans la bibliothèque standard :

instance Functor (Either a) where
    fmap f (Right x) = Right (f x)
    fmap f (Left x) = Left x

Eh bien, qu’avons-nous fait là ? Vous voyez qu’on a fait d’Either a une instance, au lieu d’Either. C’est parce qu’Either a est un constructeur de types qui attend un paramètre, alors qu’Either en attend deux. Si fmap était spécifiquement pour Either a, elle aurait pour signature (b -> c) -> Either a b -> Either a c, parce que c’est identique à (b -> c) -> (Either a) b -> (Either a) c. Dans l’implémentation, on a mappé sur le constructeur de valeurs Right, mais pas sur Left. Pourquoi cela ? Eh bien, si on retourne à la définition d’Either a b, c’est un peu comme :

data Either a b = Left a | Right b

Si l’on voulait mapper une fonction sur les deux à la fois, a et b devraient avoir le même type. Ce que je veux dire, c’est que si on voulait mapper une fonction qui transforme une chaîne de caractères en chaîne de caractères, que b était une chaîne de caractères, mais que a était un nombre, ça ne marcherait pas. Aussi, en voyant ce que serait le type de fmap s’il n’opérait que sur des valeurs Either, on voit que le premier paramètre doit rester le même alors que le second peut changer, et c’est le constructeur de valeurs Left qui actualise ce premier paramètre.

Cela va bien de pair avec notre analogie de la boîte, si l’on imagine que Left est une boîte vide sur laquelle un message d’erreur indique pourquoi elle est vide.

Les maps de Data.Map peuvent aussi être faites foncteurs puisqu’elles contiennent (ou non !) des valeurs. Dans le cas de Map k v, fmap va mapper une fonction de type v -> v' sur une map de type Map k v et retourner une map de type Map k v'.

Essayez de deviner comment Map k est fait instance de Functor par vous-même !

Avec la classe Functor, on a vu comment les classes de types peuvent représenter des concepts d’ordre supérieur plutôt cools. On a aussi pratiqué un peu plus l’application partielle sur les types et la création d’instances. Dans un des chapitres suivants, on verra quelques lois qui s’appliquent sur les foncteurs.

Sortes et un peu de type-fu

Les constructeurs de types prennent d’autres types en paramètres pour finalement produire des types concrets. Ça me rappelle un peu les fonctions, qui prennent des valeurs en paramètres pour produire des valeurs. On a vu que les constructeurs de types peuvent être appliqués partiellement (Either String est un constructeur de types qui prend un type et produit un type concret, comme Either String Int), tout comme le peuvent les fonctions. C’est effectivement très intéressant. Dans cette section, nous allons voir comment définir formellement la manière dont les constructeurs de types sont appliqués aux types, tout comme nous avions défini formellement comment les fonctions étaient appliquées à des valeurs en utilisant des déclarations de type. Vous n’avez pas nécessairement besoin de lire cette section pour continuer votre quête magique d’Haskell, et si vous ne la comprenez pas, ne vous inquiétez pas. Cependant, comprendre ceci vous donnera une compréhension très poussée du système de types.

Donc, les valeurs comme 3, "YEAH", ou takeWhile (les fonctions sont aussi des valeurs, puisqu’on peut les passer et les retourner) ont chacune un type. Les types sont des petites étiquettes que les valeurs transportent afin qu’on puisse raisonner sur leur valeur. Mais les types ont eux-même leurs petites étiquettes, appelées sortes. Une sorte est plus ou moins le type d’un type. Ça peut sembler bizarre et déroutant, mais c’est en fait un concept très cool.

Que sont les sortes et à quoi servent-elles ? Eh bien, examinons la sorte d’un type à l’aide de la commande :k dans GHCi.

ghci> :k Int
Int :: *

Une étoile ? Comme c’est bizarre. Qu’est-ce que cela signifie ? Une * signifie que le type est un type concret. Un type concret est un type qui ne prend pas de paramètre de types, et les valeurs ne peuvent avoir que des types concrets. Si je devais lire * tout haut (ce qui n’a jamais été le cas), je dirais juste étoile ou type.

Ok, voyons maintenant le type de Maybe.

ghci> :k Maybe
Maybe :: * -> *

Le constructeur de types Maybe prend un type concret (comme Int) et retourne un type concret comme Maybe Int. Et c’est ce que nous dit cette sorte. Tout comme Int -> Int signifie qu’une fonction prend un Int et retourne un Int, * -> * signifie qu’un constructeur de types prend un type concret et retourne un type concret. Appliquons Maybe à un paramètre de type et voyons la sorte du résultat.

ghci> :k Maybe Int
Maybe Int :: *

Comme prévu ! On a appliqué Maybe à un paramètre de type et obtenu un type concret (c’est ce que * -> * signifie). Un parallèle (bien que non équivalent, les types et les sortes étant des choses différentes) à cela est, lorsque l’on fait :t isUpper et :t isUpper 'A'. isUpper a pour type Char -> Bool et isUpper 'A' a pour type Bool, parce que sa valeur est simplement True. Ces deux types ont tout de même pour sorte *.

On a utilisé :k sur un type pour obtenir sa sorte, comme on a utilisé :t sur une valeur pour connaître son type. Comme dit précédemment, les types sont les étiquettes des valeurs, et les sortes les étiquettes des types, et on peut voir des parallèles entre les deux.

Regardons une autre sorte.

ghci> :k Either
Either :: * -> * -> *

Aha, cela nous indique qu’Either prend deux types concrets en paramètres pour produire un type concret. Ça ressemble aussi à la déclaration de type d’une fonction qui prend deux choses et en retourne une troisième. Les constructeurs de types sont curryfiés (comme les fonctions), donc on peut les appliquer partiellement.

ghci> :k Either String
Either String :: * -> *
ghci> :k Either String Int
Either String Int :: *

Lorsqu’on voulait faire d’Either une instance de Functor, on a dû l’appliquer partiellement parce que Functor voulait des types qui attendent un paramètre, alors qu’Either en prend deux. En d’autres mots, Functor veut des types de sorte * -> * et nous avons dû appliquer partiellement Either pour obtenir un type de sorte * -> * au lieu de sa sorte originale * -> * -> *. Si on regarde à nouveau la définition de Functor :

class Functor f where
    fmap :: (a -> b) -> f a -> f b

on peut voir que f est utilisé comme un type qui prend un type concret et produit un type concret. On sait qu’il doit produire un type concret parce que ce type est utilisé comme valeur dans une fonction. Et de ça, on peut déduire que les types qui peuvent être amis avec Functor doivent avoir pour sorte * -> *.

Maintenant, faisons un peu de type-fu. Regardez cette classe de types que je vais inventer maintenant :

class Tofu t where
    tofu :: j a -> t a j

Wow, ça a l’air bizarre. Comment ferions-nous un type qui soit une instance de cette étrange classe de types ? Eh bien, regardons quelle sorte ce type devrait avoir. Puisque j a est utilisé comme le type d’une valeur que la fonction tofu prend en paramètre, j a doit avoir pour sorte *. En supposant que a a pour sorte *, alors j doit avoir pour sorte * -> *. On voit que t doit aussi produire un type concret et doit prendre deux types. Et sachant que a a pour sorte * et que j a pour sorte * -> *, on infère que t doit avoir pour sorte * -> (* -> *) -> *. Ainsi, il prend un type concret (a), un constructeur de types qui prend un type concret (j) et produit un type concret. Wow.

OK, faisons alors un type qui a pour sorte * -> (* -> *) -> *. Voici une façon d’y arriver.

data Frank a b  = Frank {frankField :: b a} deriving (Show)

Comment sait-on que ce type a pour sorte * -> (* -> *) -> * ? Eh bien, les champs des TAD (types abstraits de données) doivent contenir des valeurs, donc doivent avoir pour sorte *, évidemment. On suppose * pour a, ce qui veut dire que b prend un paramètre de type et donc sa sorte est * -> *. On connaît les sortes de a et b, et puisqu’ils sont les paramètres de Frank, on voit que Frank a pour sorte * -> (* -> *) -> *. Le premier * représente a et le (* -> *) représente b. Créons quelques valeurs de type Frank et vérifions leur type.

ghci> :t Frank {frankField = Just "HAHA"}
Frank {frankField = Just "HAHA"} :: Frank [Char] Maybe
ghci> :t Frank {frankField = Node 'a' EmptyTree EmptyTree}
Frank {frankField = Node 'a' EmptyTree EmptyTree} :: Frank Char Tree
ghci> :t Frank {frankField = "YES"}
Frank {frankField = "YES"} :: Frank Char []

Hmm. Puisque frankField a un type de la forme a b, ses valeurs doivent avoir des types de forme similaire. Ainsi, elles peuvent être Just "HAHA", qui a pour type Maybe [Char] ou une valeur ['Y', 'E', 'S'], qui a pour type [Char] (si on utilisait notre propre type liste, ce serait List Char). Et on voit que les types des valeurs Frank correspondent bien à la sorte de Frank. [Char] a pour sorte * et Maybe a pour sorte * -> *. Puisque pour être une valeur, elle doit avoir un type concret et donc entièrement appliqué, chaque valeur Frank blah blaah a pour sorte *.

Faire de Frank une instance de Tofu est plutôt facile. On voit que tofu prend un j a (par exemple un Maybe Int) et retourne un t a j. Si l’on remplaçait j par Frank, le type résultant serait Frank Int Maybe.

instance Tofu Frank where
    tofu x = Frank x

ghci> tofu (Just 'a') :: Frank Char Maybe
Frank {frankField = Just 'a'}
ghci> tofu ["HELLO"] :: Frank [Char] []
Frank {frankField = ["HELLO"]}

Pas très utile, mais bon pour l’entraînement de nos muscles de types. Encore un peu de type-fu. Mettons qu’on ait ce type de données :

data Barry t k p = Barry { yabba :: p, dabba :: t k }

Et maintenant, on veut créer une instance de Functor. Functor prend des types de sorte * -> * mais Barry n’a pas l’air de cette sorte. Quelle est la sorte de Barry ? Eh bien, on voit qu’il prend trois paramètres de types, donc ça va être something -> something -> something -> *. Il est prudent de considérer que p est un type concret et a pour sorte *. Pour k, on suppose *, et par extension, t a pour sorte * -> *. Remplaçons les something plus tôt par ces sortes, et l’on obtient (* -> *) -> * -> * -> *. Vérifions avec GHCi.

ghci> :k Barry
Barry :: (* -> *) -> * -> * -> *

Ah, on avait raison. Comme c’est satisfaisant. Maintenant, pour rendre ce type membre de Functor il nous faut appliquer partiellement les deux premiers paramètres de type de façon à ce qu’il nous reste un * -> *. Cela veut dire que le début de la déclaration d’instance sera : instance Functor (Barry a b) where. Si on regarde fmap comme si elle était faite spécifiquement pour Barry, elle aurait pour type fmap :: (a -> b) -> Barry c d a -> Barry c d b, parce qu’on remplace juste les f de Functor par Barry c d. Le troisième paramètre de type de Barry devra changer, et on voit qu’il est convenablement placé dans son propre champ.

instance Functor (Barry a b) where
    fmap f (Barry {yabba = x, dabba = y}) = Barry {yabba = f x, dabba = y}

Et voilà ! On vient juste de mapper f sur le premier champ.

Dans cette section, on a eu un bon aperçu du fonctionnement des paramètres de types et on les a en quelque sorte formalisés avec les sortes, comme on avait formalisé les paramètres de fonctions avec des déclarations de type. On a vu qu’il existe des parallèles intéressants entre les fonctions et les constructeurs de types. Cependant, ce sont deux choses complètement différentes. En faisant du vrai Haskell, vous n’aurez généralement pas à travailler avec des sortes et à inférer des sortes à la main comme on a fait ici. Généralement, vous devez juste appliquer partiellement * -> * ou * à votre type personnalisé pour en faire une instance d’une des classes de types standard, mais il est bon de savoir comment et pourquoi cela fonctionne. Il est aussi intéressant de s’apercevoir que les types ont leur propre type. Encore une fois, vous n’avez pas à comprendre tout ce qu’on vient de faire pour continuer à lire, mais si vous comprenez comment les sortes fonctionnent, il y a des chances pour que vous ayez développé une compréhension solide du système de types d’Haskell.